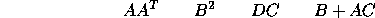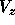 in parallel, Fig 1
in parallel, Fig 1
Comp Neuroscience
Neural processes are dynamic phenomena, which means that they change in time. These temporal variations are extremely important; indeed, many sensory stimuli are coded according tho firing rates of the neurons and not their absolute membrane potentials. The most accepted models of memory and learning depend on the rates of change of the neurons, that is, the correllation between the activities of the post- and pre-synaptic cells. Recent evidence has pointed to the importance of 40 Hz oscillations in binding diverse properties of visual and olfactory stimuli. Dynamic phenomena play an obvious role in motor activity as well. Locomotion, whether stereotypical, such as trotting of horses and grinding of the lobster stomato-gastric system, or driven by feedback, as in navigation of an obstacle course, depends on precise temporal relations between the limbs and the various components of the locomotor event. Autonomic processes such as breathing, hormonal secretion, circadian cycles, and others also depend on temporal processes such as regular rhythms and more complex phemonena, e.g. spike bursts and irregular activity.
Many pathologies are due to temporal difficulties in neural systems; notable among these are epilepsy, Parkinsonian seizures, and various EEG abnormalities. Indeed, the EEG is nothing more than a time series of the lumped activity of many active neurons.
The language of dynamic phenomena is differential equations. A
differential equation is an equation that relates the rate of
change of some process to other processes that are changing in
time. The simplest example and one that will play a role in
neurobiology is the decay to rest of the membrane potential. A
passive membrane can be modeled by a capacitor with capacitance
C and a resistor with resistance R and battery with
potential 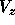 in parallel, Fig 1
in parallel, Fig 1
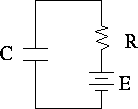
Figure 1: Passive Membrane Model
The quantity of interest is the voltage across the capacitor,
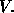 This voltage slowly leaks out of the capacitor across the
resistor. Elementary circuit theory tells us that the rate of
change of the voltage is proportional to minus the voltage difference. The
rate of change of a quantity,
This voltage slowly leaks out of the capacitor across the
resistor. Elementary circuit theory tells us that the rate of
change of the voltage is proportional to minus the voltage difference. The
rate of change of a quantity, 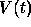 with respect to time is of
course the derivative of that quantity with respect to time.
Thus, our statement above can be translated into mathematics to
read as follows:
with respect to time is of
course the derivative of that quantity with respect to time.
Thus, our statement above can be translated into mathematics to
read as follows:
where 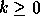 is the constant of proportionality. For the
circuit here, the constant is
is the constant of proportionality. For the
circuit here, the constant is 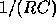 , where R is the
resistance in ohms and C is the capacitance in farads. Note
that the product of one ohm with one farad has the value of one
second. The quantity, RC is called the membrane time-constant.
Thus, a membrane with
, where R is the
resistance in ohms and C is the capacitance in farads. Note
that the product of one ohm with one farad has the value of one
second. The quantity, RC is called the membrane time-constant.
Thus, a membrane with 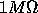 resistance and
resistance and
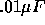 capacity would have a time constant of 10 ms. The
objective of the theory of differential equations is to try to
understand the behavior of systems like (1) and to use this
knowledge to predict the behavior of experiments. There are at
least 5 different levels at which one can study (1):
capacity would have a time constant of 10 ms. The
objective of the theory of differential equations is to try to
understand the behavior of systems like (1) and to use this
knowledge to predict the behavior of experiments. There are at
least 5 different levels at which one can study (1):
Equation (1) is called a first order differential equation (ODE) and in order to solve it, we must specify one more condition. To see why, suppose I tell you that someone is driving at 50 MPH down the turnpike. After one hour, how many miles down the pike is he? To answer this, you must know what milepost he started at. That is, you must be given the initial position. In general, you must specify an initial condition for each first order differential equation. Thus, we must give the initial voltage in the capacitor in order to solve (1). Equation (1) is of the following form:
which can be solved by integration:

so, we get:
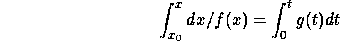
For the above equation 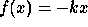 and
and 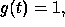 hence:
hence:
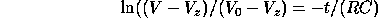
Inverting this equation, we obtain:
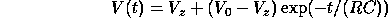
The voltage decays exponentially from its initial value. The larger the resistance, the slower it decays.
HOMEWORK
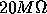 and
a capacitance of 120 picofarads. The initial potential is 100
mV and the battery is -60mV (a) What is the membrane time constant. (b) What is the
potential drop after 100 msec. (c) After how long has the
potential dropped to 25 mV.
and
a capacitance of 120 picofarads. The initial potential is 100
mV and the battery is -60mV (a) What is the membrane time constant. (b) What is the
potential drop after 100 msec. (c) After how long has the
potential dropped to 25 mV.
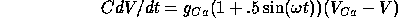
(a) Assuming that 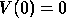 , what is the potential as a function of
time. (b) What are the dimensions of all the parameters. (c) As
, what is the potential as a function of
time. (b) What are the dimensions of all the parameters. (c) As
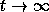 , what does the membrane potential tend to? (d) If
, what does the membrane potential tend to? (d) If
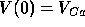 , does the voltage ever change?
, does the voltage ever change?
There are usually many differential equations in a model system. Consider the following psychological example. Suppose that Harry is a fickle suitor and Sally is the woman who he is interested in. The rate at which her love for him changes depends on his love for her. Harry on the other hand is interested only when she is not and loses interest as soon as she finds him attractive. Let x denote the amount that Harry is attracted to Sally and let y denote the amount that Sally is attracted to Harry. Then the equations are:
If 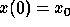 and
and 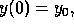 then it is simple to verify that
the solution to (3) is:
then it is simple to verify that
the solution to (3) is:
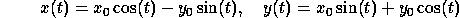
The point is not that this equation is solvable, but rather that it typifies the interactions of ``excitatory'' and ``inhibitory'' processes. The variable y ``inhibits'' x and x ``excites'' y as in Fig 2.

Figure 2: Typical negative feedback interaction
This type of interaction often leads to oscillations and is a form of delayed inhibition. Another way to induce a delayed inhibition is to put it in directly:
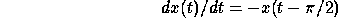
This is an example of a delay-differential equation. We will
not study these too much since they are very difficult to solve.
However, solution to this problem is 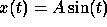 We will see
later that this notion of delayed inhibitory feedback is responsible for
most if not all oscillatory behavior in neurons.
We will see
later that this notion of delayed inhibitory feedback is responsible for
most if not all oscillatory behavior in neurons.
Now consider a general system of two linear differential equations:

The general solution to this equation (except for some special cases) is:
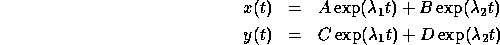
where A,B,C,D are constants (perhaps complex) that depend on
the initial conditions and the parameters a,b,c,d and
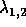 are the eigenvalues of the 2x2 matrix:
are the eigenvalues of the 2x2 matrix:

Recall that the eigenvalues of a matrix M are the roots of the characteristic polynomial which is

where I is the identity matrix of all zeros except the 1's along the diagonals. For the present example,
This second degree polynomial has two roots. The quantity 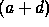 is
the trace of the matrix M and the quantity ad-bc is the
determinant of the matrix. The roots of the polynomial can be
either real or complex. If the real parts are positive, then it is
clear that the solutions
is
the trace of the matrix M and the quantity ad-bc is the
determinant of the matrix. The roots of the polynomial can be
either real or complex. If the real parts are positive, then it is
clear that the solutions 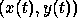 will grow exponentially fast as
t
increases. Thus, the solutuion will not be bounded. On the other
hand, if all the real parts are less than or equal to zero, then the
solutions will remain bounded as
will grow exponentially fast as
t
increases. Thus, the solutuion will not be bounded. On the other
hand, if all the real parts are less than or equal to zero, then the
solutions will remain bounded as  As an example, the
Harry-Sally problem has
As an example, the
Harry-Sally problem has 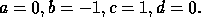 So that the
eigenvalue equation is:
So that the
eigenvalue equation is:

The roots of this are 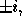 where
where 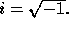 Since
Since 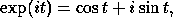 we see that we recover the originally found solutions.
we see that we recover the originally found solutions.
HOMEWORK
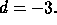
A short aside in linear algebra
Linear differential equations, which are ultimately very important
since many nonlinear systems are approximated by them near equilibria,
are solved by using techniques from linear algebra. The most crucial
ideas are the notions of eigenvalues and eigenvectors. I will assume
that you know how to multiply matrices together and that you can find
the transpose of a matrix and the inner product of two vectors.
The norm of a vector is the
square root of the sum of the squares of each element. The
inner product of two vectors is the sum of the products of
each of the elements. Just
for notational sake, A is an 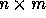 matrix means that A has
n rows and m columns. The matrix norm of A is the maximum
over all rows of A of the sums of the absolute values of the elements
in each row. A row vector is a
matrix means that A has
n rows and m columns. The matrix norm of A is the maximum
over all rows of A of the sums of the absolute values of the elements
in each row. A row vector is a 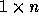 matrix and a
column vector is a
matrix and a
column vector is a 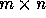 matrix. Matrices are
multiplied in the usual manner . To multiply an
matrix. Matrices are
multiplied in the usual manner . To multiply an 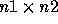 matrix
by an
matrix
by an 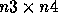 matrix, you must have n2 = n3 and the result
is an
matrix, you must have n2 = n3 and the result
is an 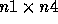 matrix. The ij entry of the product of two
matrices takes the
matrix. The ij entry of the product of two
matrices takes the 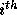 row of the first times the
row of the first times the 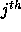 column
of the second ( ie the inner product of a row from the first with
a column from the second.)
This is why the number of columns in the first must
equal the rows in the second. A square matrix has an inverse if there
is a square matrix B such that AB=BA=I where I is the square
matrix with 1 along the diagonal and 0 everywhere else. A matrix is
invertible if and only if the determinant of that matrix is nonzero.
column
of the second ( ie the inner product of a row from the first with
a column from the second.)
This is why the number of columns in the first must
equal the rows in the second. A square matrix has an inverse if there
is a square matrix B such that AB=BA=I where I is the square
matrix with 1 along the diagonal and 0 everywhere else. A matrix is
invertible if and only if the determinant of that matrix is nonzero.
EXAMPLES
I define 4 matrices,

Note that D is a row vector. You can multiply BA but not AB
since A has 3 columns and B has 2 rows so they are not compatible.
If you multiply AC you get a 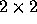 matrix,
matrix,

but if you multiply
CA you get a 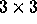 matrix
matrix

Only square matrices have inverses. It is easy to show that
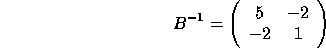
The norm of the row vector, D is 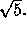 The matrix norm of A
is 6. The transpose of B is itself. We say such a matrix is
symmetric. Symmetric matrices play an important role in the theory of
``neural nets.'' The transpose of D is a column vector.
The matrix norm of A
is 6. The transpose of B is itself. We say such a matrix is
symmetric. Symmetric matrices play an important role in the theory of
``neural nets.'' The transpose of D is a column vector.
Eigenvalues
Let A be a square matrix. Often we want to find vectors v such that multiplication by A is equivalent to scalar multiplication:
where 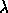 is a complex or real scalar.
If we can find pairs
is a complex or real scalar.
If we can find pairs 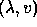 such that equation (6) holds, then we say that
such that equation (6) holds, then we say that 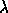 is
an eigenvalue and v is an eigenvector for
is
an eigenvalue and v is an eigenvector for 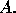 How do we solve
this problem. Subtracting, we must have:
How do we solve
this problem. Subtracting, we must have:

This is a linear system of equations. One solution is that v=0
If the matrix, 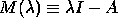 has an inverse,
then this is the only solution. Thus, we must find values of
has an inverse,
then this is the only solution. Thus, we must find values of
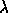 such that A is not invertible. Recall that a matrix is
noninvertible if it has a zero determinant. Thus, we take the
determinant To do this, we take the determinant
of
such that A is not invertible. Recall that a matrix is
noninvertible if it has a zero determinant. Thus, we take the
determinant To do this, we take the determinant
of
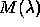 and set it to zero.
This results in a
and set it to zero.
This results in a 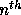 degree polynomial, the characteristic
polynomial that has n roots.
Thus, a general
degree polynomial, the characteristic
polynomial that has n roots.
Thus, a general 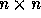 matrix has n eigenvalues.
matrix has n eigenvalues.
Eigenvalues are either real or complex. A matrix which satisfies
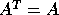 that is it is its own transpose (i.e. symmetric) always
has real eigenvalues.
EXAMPLE
that is it is its own transpose (i.e. symmetric) always
has real eigenvalues.
EXAMPLE
The matrix A from the above examples is symmetric. Since A is
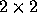 , it follows that the characteristic polynomial is given by
(5) so the eigenvalues satisfy:
, it follows that the characteristic polynomial is given by
(5) so the eigenvalues satisfy:

whose solutions are 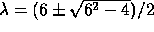 or
or
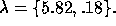
HOMEWORK