![]()
home
::: about
::: news
::: links
::: giving
::: contact
![]()
events
::: calendar
::: lunchtime
::: annual
lecture series
::: conferences
![]()
people
::: visiting fellows
::: postdoc fellows
::: resident fellows
::: associates
![]()
joining
::: visiting fellowships
::: postdoc fellowships
::: senior fellowships
::: resident fellowships
::: associateships
![]()
being here
::: visiting
::: the last donut
::: photo album
|
Exorcising Maxwell's Demon
It is generally good advice to rehearse a talk before you give it; and it is better to rehearse before a sympathetic audience. Next week, I will head off to San Diego to give a talk on Maxwell's demon. Why not try it out this week in my home territory? With that in mind, I decided to fill a vacancy in our lunchtime talk series.
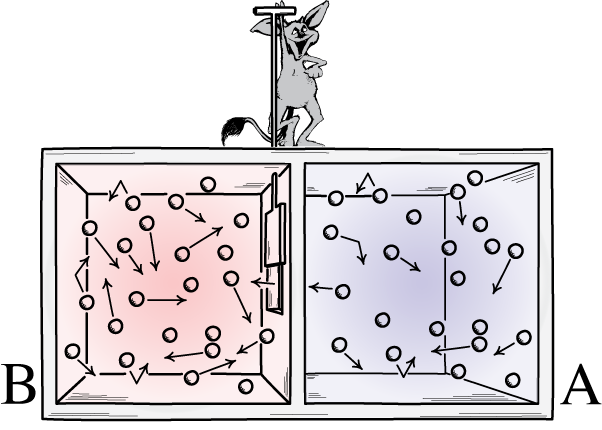
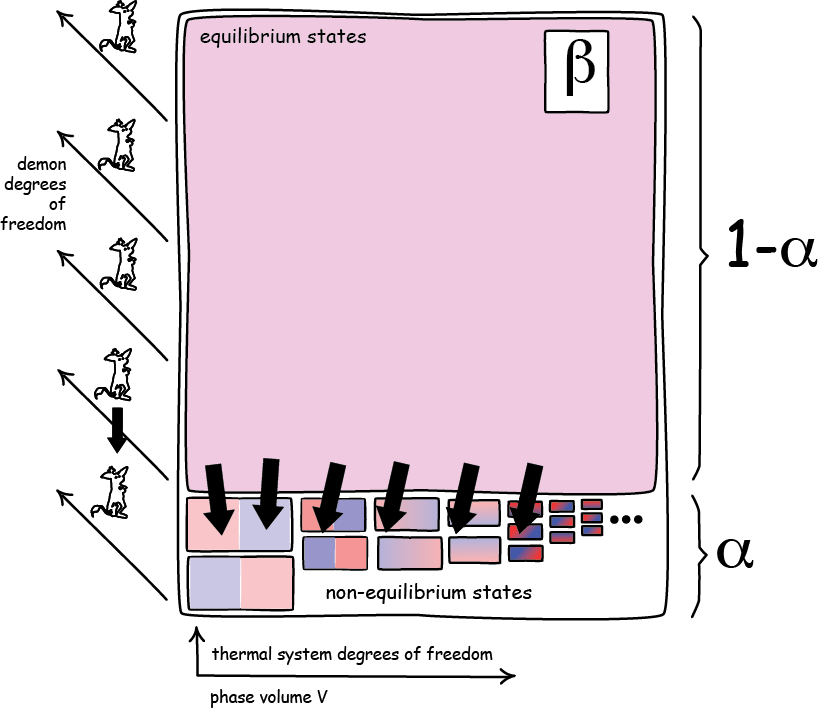
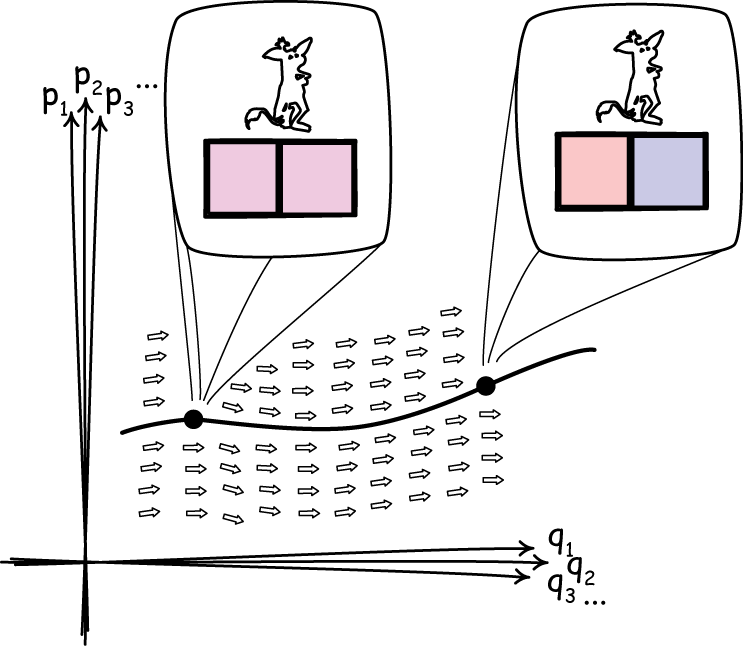
A Center audience here in Pittsburgh should match that mix pretty well. My sense that this would be so was affirmed when someone asked me in the hallway prior to the talk, "Will you be talking about Maxwell's equations?" I had set up the computer well ahead of the talk. By the time I made it back to the conference room, I found a good audience assembling. I took a photo of the speaker's view, as people still settled in their seats. Just keeping records for the website! Then I was startled and pleased to see that someone had written a welcome in large letters on the whiteboard. I quipped that it was a better class of graffiti including my name than I was used to. (Giovanni Valente later admitted that he had put it up.) What was my talk about? Working initially with John Earman in the late 1990s, I've been thinking and writing about Maxwell's demon for a long time. Last summer, however, I'd stumbled onto something so strong and simple that it took me a while to realize that it had been overlooked in the literature for many decades. My goal was to present and explain that result. It is a very short way to show that a Maxwell's demon is impossible that makes no use of the dominant notion in the present literature, information. But first I wanted to give some historical background to help those who have trouble separating Maxwell's demon from Maxwell's equations. The demon, as many of you know, is a tiny "neat fingered" being imagined in the mid 19th century by James Clerk Maxwell as able to see the motions of individual molecules in a gas. As a result, the demon can cleverly open and shut a door in a partition in a vessel containing the gas so that the faster molecules collect on one side while the slower molecules collect on the other. The net effect is a separation of hot from cold and a violation of the second law of thermodynamics. Maxwell himself was untroubled by this outcome. That's just the way things go when you have tiny beings that can work with individual molecules, he thought. Stuff happens. Laws break. However a later tradition was disconcerted. It felt compelled to find reasons for why the demon could not reverse the second law of thermodynamics. Starting with a path breaking paper by Leo Szilard in 1929, that reason has become "information." In its first incarnation, Szilard, von Neumann, Brillouin and others note that a demon must acquire information about the gas to function. In doing this, they presumed, the demon must create thermodynamic entropy in quantities that protect the second law. Their tradition was eclipsed in the 1980s by Bennett, who drew on earlier work of Landauer. He now argued that there is no necessary dissipation in acquiring information. Szilard, von Neumann and the others just got it wrong. Rather the necessary dissipation that protects the second law comes when the demon returns to its initial state and erases its memory. This is now the standard view among people who publish views on the matter. This information-based tradition is appealing, initially. However, as I found when John Earman and I began working on it years ago, closer examination revealed frailties and oddities. Still closer examination yields more problems until you see reluctantly that the entire tradition is confused and based on misapplications of statistical physics. Or so I have argued in a series of papers that are collected on my website here. What do I now have to add to this? While the debates over information, entropy and Maxwell's demon have raged, we focussed too much on information. The information proponents were too eager to make the failing idea work; and the information skeptics--me included--were too eager to show that the idea fails. What happens if we just forget about information and ask the simple question, can the demon succeed? It turns out that there there is a simple answer if we restrict ourselves to classical physics: It cannot. The demonstration requires some assumptions, none of them remarkable. The upshot is simple. If we just describe carefully what a Maxwell's demon must do in very general terms, it turns out that the description violates a simple, but quite general theorem of Hamiltonian mechanics: Liouville's theorem. I won't repeat the details here. They are laid out well enough in a brief account on my website here. As it turns out, I can tell the story quite precisely with essentially no mathematical formalism. It is all done with the notion of a phase space whose volumes can move around but can never be compressed or expanded. This is the technical part of the talk and my hope is that the simplicity of the manipulations will be clear to all. I show colored spaces with arrows and tell stories about how this part cannot be compressed into that... so the demon cannot succeed.
Keeping to time is always a problem in giving a talk. Somehow this one ended a little sooner than I expected: 38 minutes, where I'd expected over 45. I made a mental note for San Diego. "You can slow it down a little." Now came question time. Did the talk work? Did it get through to technical types and non-technical types? Others should and perhaps have already made the final judgment. However, my sense is that it did. The less technical types were pressing me on details of the spaces used in the arguments. Just how, they asked again, does it work? It is, I began to see, not so easy to make the jump from a three dimensional space in which a great cloud of molecules move about to a phase space of immensely high dimensionality in which that same motion is captured by a single point moving along a line.
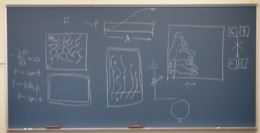
It was an energetic question time. Several times I raised the projector screen so I could draw figures in chalk on the blackboard.
The experts pressed me on expert issues. How does my story fit with the normal account of how thermal equilibrium is achieved? If phase space cannot expand, how do we go from non-equilibrium to equilibrium states? What about Poincaré recurrence? Isn't there still room for information talk? And more. What I was listening for was the thing that every speaker dreads: the subtle twist of logic that you sped past too hastily; the small, unnoticed hole that sinks the ship. As the questioning proceeded, I was relaxing. The hole never came. Indeed the worst threat came from the reverse direction. Bob Griffith, himself an expert in thermal physics, was starting to push me towards the idea that the result was merely a recapitulation of a demonstration of the second law. There's nothing new in that. While I resisted the idea that the analysis was merely that, it was a quite comforting line. It reassured me that the analysis looked solid. Some forty minutes after the question time officially ended, I was still in energetic conversation in the conference room when Karen quietly slipped in. Did I forget that we had a Center staff meeting... ? Oops, yes, I'd forgotten. John D. Norton Thanks to Carrie Figdor and Arnaud Pocheville for taking photos.
|