

![]()
home
::: about
::: news
::: links
::: giving
::: contact
![]()
events
::: calendar
::: lunchtime
::: annual
lecture series
::: conferences
![]()
people
::: visiting fellows
::: postdoc fellows
::: resident fellows
::: associates
![]()
joining
::: visiting fellowships
::: postdoc fellowships
::: senior fellowships
::: resident fellowships
::: associateships
![]()
being here
::: visiting
::: the last donut
::: photo album
|
|
Dice
Feb.27, 2015
After Charlotte Werndl had finished her Annual Lecture Series talk “On Defining Climate and Climate Change,” she, Eric Winsberg and I were hovering in the hall in the relaxed state that comes after an hour’s talk and then almost that long in energetic questions.
I was explaining the reason for the glass boards in the hall and then took the opportunity to solicit another response to my survey about Bayesianism and inductive inference.
The survey has a rather inept drawing of a die. In a moment of haste, I’d put it there for visual interest, so that there would be at least one picture. Eric glanced at the die and said, “It’s wrong!”

Eric was bothered by this, as he should be. Recognizing one of my type, I chided him for his obsession with such details. Then things got interesting.
Just why do we have the sum rule?
That stumped us. The first reaction is that it balances the die. But that definitely isn’t it. The sum rule does the opposite. On the six face, we drill out 6 holes making it the lightest face. We pair it with the face that has just one hole drilled out. That is the heaviest face. We have now assured the worst imbalance possible.
We had soon roped Wayne into the discussion. “Just tradition,” he asserted with some confidence; and that will likely prove in the long run to be the right answer.
After a lively exchange, we parted. But the worry about the sum rule stuck. Since the cube is perfectly symmetric, there is no obvious reason for any rule on how the numbers should be distributed. Soon we were in an energetic email exchange. It turns out that one can cook up a few quite plausible “just so” stories.
Before the perfectly cubical dice, there were knucklebones-—“astragali.” They were used as game pieces and, sometime, crude dice. They are not perfectly symmetric. They have two opposed large sides and two opposed smaller sides over which four values could be distributed.
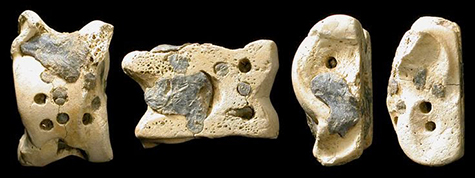
These larger sides would come up more often. That could be bad. What if these favored sides of one astragalus turns out to be bigger than those of another? That first astragalus would then be more likely land on one of these favored sides. That would mean that different astragali would behave differently in repeated tosses.
There’s simple way to minimize that undesirable effect. Use a version of the sum rule: put the highest and lowest values on these two largest sides.
With the transition to cubical dice, might this rule just be carried over, even though it was no longer needed?
That seemed plausible. But Eric found a complication: he found ancient Roman dice that did and did not obey the rule. Things were not so clear, since the earliest dice did obey the sum rule, but not the later ones.


What?! Might the earliest dice have preserved the rule, but then it was dropped in the later ones when it was realized that it was no longer needed?
But then why was it brought back?
Eric again found what might be the best answer. In a website on cheating with dice, he found about about “axial control.”
Let’s say you toss the die so it rolls across the table like a wheel, with the 6-1 axis horizontal, like the axle of a wheel. Then the faces on the rim of the wheel are 5, 3, 2, 4. When the wheel stops, it will surely be on one of those numbers. The average, however, will still be the 3.5 of a regular throw. So you have reduced the variance, but not the mean. That is, on average, your score is no better than with a regular throw.
If the die does not respect the sum rule, however, you might not have that property. It might be possible to increase your average score and gain an advantage with “axial control.”
All this is intriguing and it remains an open puzzle.
Now that is just the thing I should put on my glass board!
That is how the glass board started. By the end of the next day, new text had appeared on it.
John D. Norton





