
| HPS 0628 | Paradox | |
Back to doc list
Paradoxes: Their Diagnosis, Treatment and Cure
John D. Norton
Department of History and Philosophy of Science
University of Pittsburgh
http://www.pitt.edu/~jdnorton
Supplementary page: The Logic of Arguments
"I am so glad I don't like asparagus,"
said the small girl to a sympathetic friend.
"Because, if I did, I should have to eat it
--and I can't bear it!"
Lewis Carroll
In the spacestation, HAL the robot repairs exactly all
those robots who do not repair themselves.
Assuming that every robot gets repaired, who repairs HAL?
A paradox is an argument that proceeds rapidly from apparently innocuous assumptions by apparently acceptable reasoning to an apparently absurd or impossible conclusion.
Most people know at least one paradox, such as the
"asparagus" paradox. Such paradoxes are usually appreciated for their
entertainment value. Who can suppress a smile at the tortured reasoning of
the girl who doesn't like asparagus? Outside
philosophical circles, one treats a paradox like a good joke.
They are to be told, enjoyed and then, before the smile has completely
faded, one moves on to something else. Perhaps there is a fear that one
can ruin a good paradox by dwelling on it, in the way that one can ruin a
good joke by laboring it. Philosophers know better. The initial moment of
delight when a good paradox is encountered is just the beginning.
To the philosopher, a good paradox is a challenge. The philosopher
cannot simply brush off a paradox with a "well, fancy that!" For
a good paradox pretends to show us how innocuous assumptions and sound
reasoning lead rapidly to absurdity. That we can generate absurdity so
easily is a direct challenge to the most fundamental tool of virtually all
human activity, clear reasoning and thought. There must be some trick in
every paradox that makes the failure of reason nothing more than a
deceptive appearance.
The alternative is quite disastrous. It is to admit that reason is unreliable. It is to admit that whenever we undertake even the simplest of inferences we walk the precarious edge of a deep abyss. We may arrive at sensible conclusions from sensible assumptions--the flash of fire and the puff of smoke may allow us to conclude that our aging toaster has finally broken. Or, for no discernible cause, we may fall into the abyss and arrive at the wildest absurdity. ("It is a good thing that the toaster blew up. Otherwise, we have to continue using it--and that would not be good since it is broken. Let us hope our new toaster blows up soon too!")

The task of the philosopher
is to rescue reason and find exactly where the trick lies. Some paradoxes,
such as "asparagus," yield rapidly to brief reflection. Others require a
more careful and systematic assault. These more difficult paradoxes enable
us to sharpen our most valuable of philosophical skills, the ability to
formulate good arguments validly and lucidly. Some are so deviously
constructed that they present a very significant challenge--and it is hard
to beat the satisfaction of cracking them!
Efforts put into disentangling the logic of paradoxes can repay us
handsomely. They can lead us directly to some of the most profound
revelations in philosophy, science and mathematics. We will learn from
them that
• a set cannot just be a collection of anything you please;
• we can reason reliably with infinities, but ...
• ... the notion of infinity is far more complex than anyone could have imagined, containing within it infinity upon infinity of hierarchies of infinities;
• many things we think we can do, we cannot;
• computers are profoundly limited in what they can do even if we give them unlimited memory and computing time; and
• our intuitive notion of chance needs to be corrected by probability theory; and
• and the notion of chance itself is bigger than probability theory.
In order to disentangle a paradox, the most important thing is to discover the nature of the absurdity that arises. There are two possibilities that are to be handled very differently:
In many cases, the paradox depends on arriving at a result that merely seems absurd. The treatment of such a paradox does not require us to revise the paradox itself. Rather the treatment should focus on us. We should determine what intuitions have falsely led us to decide that the result is absurd. Often this process is extremely helpful in so far as it helps us reveal false and unnecessarily restrictive assumptions that we may harbor.
The term "paradox" has a somewhat fluid meaning. To
some, the revelation that the absurd result is really quite acceptable
amounts to revealing that it was not a "true" paradox after all.
In the more troublesome cases, the absurdity of a paradox arises through a contradiction. That is, the paradox has started with apparently innocuous assumptions and, through apparently innocuous reasoning, arrives at a contradiction.
If we are serious about using reason as a tool, we
cannot tolerate the generation of contradictions. If we did, which of the
two contradictory conclusions are we to believe? Both are supported by
apparently sound reasoning. But we certainly cannot accept both!
Paradoxes of this type have proven to be especially important in
mathematics and logic, sometimes opening entire new fields of study. In
this context, they are sometimes called "antinomies."
The treatment and cure of paradoxes of this type is very different from
the first type. They are not paradoxes that we learn to live with by
retraining our intuitions. Something has gone very wrong in the reasoning
that generated the contradiction and our task is to find out what it is.
Three are two possibilities only:
• The reasoning proceeds from assumptions that contradict. (Thus not all of them can be true.)
• The reasoning is fallacious. (That is, the reasoning violates the rules of logic.)
or both.

https://commons.wikimedia.org/wiki/File:Poiuyt--opaque.svg https://commons.wikimedia.org/wiki/File:Penrose_stairs_artwork_SPL.jpg https://commons.wikimedia.org/wiki/File:Reutersvärd’s_triangle.svg
The simplest examples
of paradoxes whose absurdities are only apparent are the first few of the
Budget of Paradoxes:
• Paradoxical figures
• One hand clapping
In each case, there is merely a suggestion of something troublesome.
The paradoxical figures misuse the conventions of drawing in perspective to produce a two dimensional image of something that cannot exist in three dimensions.
We all know that one hand cannot make a clapping sound (by ordinary means). The query "What is the sound of one hand clapping?" momentarily makes us think otherwise. When we realize we have been tricked, the appearance of absurdity disappears.
That some problem leads to an infinite regress might seem to be fatal. It is easy to take the appearance of an infinity in the problem as unrecoverable. However that is not so, unless one has the untenable view that the notion of infinity itself is somehow internally contradictory.
Rather, when some problem arrives at an infinite regress, if we want to use it to dismiss the result as untenable, we have a positive obligation to show that this infinity is fatal.
In common cases, the infinity fails to be fatal. Consider again the chicken and the egg of the Budget of Paradoxes. The paradox depends on a very simple biological theory. Chickens always hatch from eggs; and eggs are always laid by (matured) chickens. This oversimplified theory admits an equally simple history of egg-chicken-egg-chicken-... and so on infinitely into the past. Unless we are to dismiss anything infinite, there is no internal difficulty.
The problem arises when we recall, tacitly, that our earth has only a finite past. However to recall that and nothing more is to be highly selective in just which facts we import from the world. If we are to introduce this fact, then we should also introduce more facts about the evolutionary origin of birds on our earth. As we trace back through the eons of biological history, we would find our chickens evolving from more primitive life forms. The change would be so gradual that, without arbitrariness, we could not declare any one chicken-like being or egg-like structure as the first.
It is the same with "turtles
all the way down." The mere fact of an infinity of turtles is
not, by itself, grounds for dismissing the notion. It does turn out that
this infinite structure can be configured so that it conforms with a
simple Newtonian, gravitational physics. The details can be found here.

My impression is that most cases of infinite regresses are benign. There are, however, truly troublesome cases. The most celebrated arises in Hume's notorious problem of induction. The challenge is to justify some rule of inductive inference. The common starting point is the rule of enumerative induction. From finding some A's are B, we are to infer that all A's are B. In the regress version of the problem presented by Popper, we justify this rule by applying a second rule to it; we then justify this second rule by means of a third rule; and so on infinitely. The difficulty is that no rule is ever properly justified. Each rule derives its justification from the next rule in the regress; and so on.
The problem of induction resides within one of the
most expansive literatures in philosophy. For my view of it and for my
approach that I believe dissolves the problem see Chapter 6. The Problem
of Induction in The
Large-Scale Structure of Inductive Inference.
The accelerating spaceship is another example of an apparent absurdity. What supports the idea of absurdity is the sense that the spaceship always has to be somewhere in space. Even if it were to explode, the fragments would still be scattered about, each somewhere in space.
This sense is misleading. If we plot the position
of spaceship over time in a spacetime diagram, we can get a clearer view
of its motion. In the figures, following the standard conventions in
relativity theory, time is plotted up the page and space across the page.
The motion starts at time = 0. As time passes, the spaceship speeds up and its trajectory in spacetime inclines more away from the vertical to the horizontal. The schedule of acceleration is so set up that the resulting curve approaches arbitrarily close to the horizontal and in such a way that it never intersects the horizontal line at time = 1.
The trajectory has no end point. If we continued the figure to the right, the trajectory would continue to extend for as long as we have patience in extending the figure. What this means is that there is no time at which the spaceship suddenly de-materializes. There is no ending point to the trajectory. For all times in the interval 0 < time <1, it has a definite position in space. At time =1, it has no position. It isn't anywhere.
This behavior is certainly unfamiliar; and we are not likely to see anyone construct a rocket that could move in this way. It would require us to ignore the upper speed to motions imposed by relativity theory. That aside, the mere fact of a trajectory of this type is not absurd. It is merely unfamiliar.
To develop examples of arguments that arrive at a true contradiction, we need first to clarify just what is meant by an argument. If you have taken an introductory course in logic, you likely know everything needed for what follows; and a great deal more. If you are new to logic or would like a very rapid refresher, see The Logic of Arguments.
A valid (deductive) inference or argument is one in which the truth of the premises guarantees the truth of the conclusion. Valid inferences conform with the rules of logic. For example:
All professors are
people.
___Therefore, validly_______
Some professors are people.
A (deductive) fallacy
is an inference in which the truth of the premises does NOT guarantee the
truth of the conclusion. Fallacies violate the rules of logic. For
example:
Some professors know
Latin.
___Therefore, fallaciously___
All professors know Latin.
Note the correct use of
the terms: "valid" and "fallacious" apply to inferences and
arguments, not to propositions.
Right: It is a fallacy to infer that all professors
know Latin.
Wrong: It is a fallacy that all professors know Latin.
This last fallacy is easy to identify. Fancier ones appearing in paradoxes may be harder to identify. Try this one:
Premise: For any odd number, there are infinitely
many even numbers greater than it.
e.g. 1 is less than 2, 4, 6, 8, ...
3 is less than 4, 6, 8, 10, 12, ...
etc
____Therefore, fallaciously,_____
There are infinitely many more even numbers than odd numbers.

https://commons.wikimedia.org/wiki/File:Asparagus-Bundle.jpg
The "asparagus" paradox above is an easy
example of a paradox dependent on a fallacious argument. Most
people will see this without further discussion. However it is a useful
exercise to lay out the fallacy in detail. The paradox depends on two
assumptions
1. I do not like asparagus.
2. IF I like asparagus THEN I should have to eat asparagus.
There is also a third tacit
assumption
3. IF I do not like asparagus, THEN I do not have
to eat asparagus.
Clearly, this is a consistent set of assumptions.
The problem arises when the small girl makes a fallacious inference.
Either from 2. or from 1. and 2. together, the girl infers
4. I eat asparagus.
This proposition 4. cannot be inferred from the
earlier premises without committing a fallacy. What can be inferred
validly from 2. and 3. together is:
(From 2, 3) I like asparagus if and only if I should have to eat it.
This fallaciously derived
conclusion 4. contradicts a valid inference from 1. and 3.
5. I do not have to eat asparagus.
The remedy for the paradox is obvious: we disallow
the fallacious inference to 4.
Both examples in the chapter, Budget of Paradoxes depend on fallacious inferences in the form of illicit steps in an algebraic derivation.
Consider the first proof that 2=1. Stripping out all the intermediates, the proof has steps
...
Let x=1
...
(x+1)(x-1) = (x-1)
Divide both sides by (x-1):
x+1 = 1
...
Since x=1, we have that (x-1) = 0. The step "Divide both sides by (x-1)" is actually "Divide both sides by 0." Division by 0 is a poorly defined operation that gives no definite result in ordinary algebraic manipulations. As a result, division by zero takes a well-formed equality
(x+1)(x-1) = (x-1)
and converts it into
(something not well defined) ??=?? (something not well defined).
Exactly because both terms are not well defined, we cannot assert an equality. The inference shown above from (x+1)(x-1) = (x-1) to x+1 = 1 is a fallacy.
...
Let x=1
...
(x+1)(x-1) = (x-1)
Divide both sides by (x-1) and infer FALLACIOUSLY that:
x+1 = 1
...
---------oOo---------
The proof that 0=1 commits a similar fallacy.
The infinite sum 1 - 1 + 1 - 1 + 1 - 1 + ... has no definite value. The value it can have varies according to the order in which we add up the terms. The order can be specified by grouping the terms differently with parentheses. We find that the different grouping leads to different results:
(1-1) + (1-1) + (1-1) + ... = 0 + 0 + 0 + ... = 0
but
1 - (1-1) - (1-1) - (1-1) - ... = 1 - 0 - 0 - 0 - ... = 1
...
The sum is
0 = (1-1) + (1-1) + (1-1) + (1-1) + ...
We can regroup the terms in the sum as
1 - 1 + 1 - 1 + 1 - 1 + 1 - 1 + ...
1 - [(1 - 1) + (1 - 1) + (1 - 1) + ...]
It is a fallacy to infer that the sum with the new grouping equals the original sum. That is, it is a FALLACY to infer that
0 = 1 - [(1 - 1) + (1 - 1) + (1 - 1) + ...]
so that
0 = 1 - [0 + 0 + 0 ...] = 1
...
Bonus remark:
Using this fact, we can reconfigure the original argument to become a reductio
ad absurdum of the proposition that the infinite sum 1 - 1 + 1 -
1 + 1 - 1 + ... has a definite value.
The reconfigured paradox looks like this:
1. Assumption for reductio:
1 - 1 + 1 - 1 + 1 - 1 + 1 - 1 + ...
has a definite value.
2. Group the terms this way to recover a value of 0.
(1-1) + (1-1) + (1-1) + (1-1) + ... = 0
We can regroup the terms in the sum as
1 - [(1 - 1) + (1 - 1) + (1 -
1) + ...]
3. Each of the terms (1-1) equals 0. Hence the sum is:
1 - [0 + 0 + 0 ...] = 1
4. The original series has different results according to how we group
the terms. (From 2 and 3)
5. Proposition 4. contradicts the assumption 1. for reductio.
6. Assumption 1. is false.
Einstein's geometric puzzle depends upon a misdirection in the geometric manipulation. The figure is drawn in such a way as to give the impression that the four triangles and two rectangles cover both the 8x8 square and 5x13 rectangle exactly. To make the paradox work, it is essential in drawing the figures that they be just a little inaccurate. That disguises the fact that the shapes do cover the 8x8 square exactly but do not exactly cover the 5x13 rectangle.
The original figure for the 5x13 rectangle was drawn as
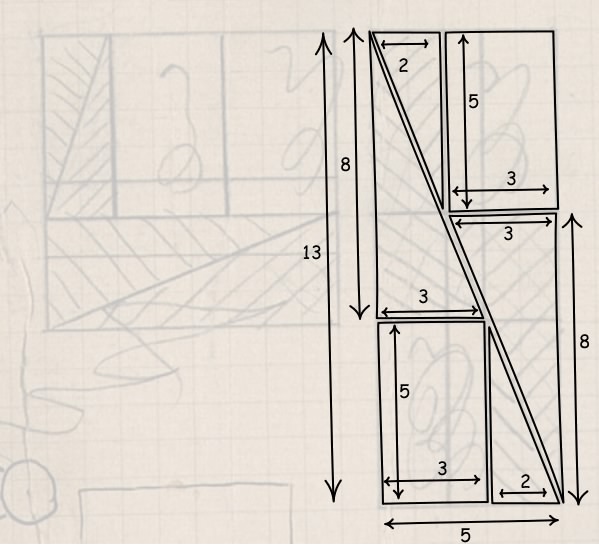
The more accurately drawn figure is:
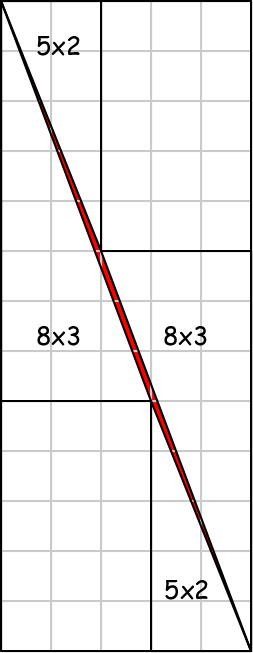
The long sides (hypotenuses) of the 8x3 and 5x2 triangles do not form a perfectly straight line, but one that is slightly bent away from the center. This leaves a slender, diagonal area, marked in red that is not covered by the transferred shapes. It comprises the unit area difference between the 8x8=64 square area and the 5x13=65 rectangular area.
It is a little hard to categorize exactly how the paradox fails to demonstrate that 64=65. The trick lies in the geometric manipulation, in the almost imperceptible errors in the figure, and not in explicit propositions. Since this trick induced us to reason poorly, I characterize the failure here as a fallacious inference. We infer fallaciously from the figures that the shapes that exactly cover the 8x8 square also exactly cover the 5x13 rectangle.
An alternative diagnosis
might be that the paradox depends on inconsistent premises:
1. The transported triangles and rectangles exactly cover the 5x13
rectangle. (from inspection of the loosely drawn figure)
2. The transported triangles and rectangles do NOT exactly cover the 5x13
rectangle. (from inspection of the carefully drawn figure)
For more, see A Peek into Einstein's Zurich Notebook
As the galaxies of space recede from one another in the paradox of the expanding universe, each volume of space loses matter over time:
This loss happens in every volume of space. The paradox arises when we are to think that this universal loss conflicts with the conservation of matter.
The inference from each volume of space losing matter to a violation of the conservation of matter is a fallacy. It is an inference that would be valid in the familiar, bounded non-expanding spaces of ordinary physics. For then if matter is diluting in one part of space, it must be concentrating somewhere else. However, in modern, relativistic cosmology, space itself is expanding. The recession of the galaxies arises when the galaxies are dragged along by the expanding space. The matter of the universe at some earlier time is merely spread over a greater volume of space. Hence its density drops everywhere without any loss of matter that would violate the conservation of matter.
This effect is illustrated in the figure. One possibility in modern cosmology is that space has a spherical geometry. That is, if space were two-dimensional, it would be just like the surface of a space. The cosmic expansion then just corresponds to the sphere growing in size. As it grows, it drags the matter of the galaxies along with it. They are shown in the figure as the black spots.
Consider the galaxies that populated the darker shaded area of the smaller spherical surface. They are dragged by the expansion to fill the larger, lighter-shaded area in the larger sphere. The original shaded area has now lost matter. But the lost matter has not been destroyed. It is merely distributed in greater dilution over a larger area of the larger surface.
The inference from each volume of space losing matter to the conclusion of a violation of the conservation of matter is a fallacy.
This same analysis applies to every area of the surface of the sphere. A similar analysis applies also to cosmologies whose overall spatial geometries are flat or hyperbolic.
This is one way to undo the paradox. We shall in the chapter on infinity that there is another way of undoing the paradox within ordinary Newtonian theory. It does not require the more exotic process of the expansion of space itself.
In these cases, the contradiction in the paradox arises because we started with contradictory assumptions. Once the contradictory assumptions are exposed, the paradox is resolved. For these cases, the air of paradox arises because the contradiction among the assumptions is sufficiently well hidden that we do not see it.
To recall:
In the spacestation, HAL the robot repairs
exactly all
those robots who do not repair themselves.
Assuming that every robot gets repaired, who repairs HAL?
https://commons.wikimedia.org/wiki/File:Cartoon_Robot.svg
The question leads to a contradiction:
If HAL repairs himself, then, since HAL only repairs robots that do not repair themselves, he does not repair himself.
Alternatively, if HAL does not repair himself,
then, since HAL is the robot who repairs exactly all those robots who do
not repair themselves, HAL must repair himself. That is, we have concluded
that
HAL does not repair himself.
HAL does repair himself.
The paradox derives from contradictory assumptions. In brief, the problem
lies in the assumption that it is possible for there to be a robot with
the properties described. This, of course, is not so easy to see. That is
why the paradox is entertaining.
At some greater length, the assumptions used in the argument are:
1. There is a set of robots. (premise)
2. Every robot is repaired by itself or one of the other robots.
(premise)
3. There is a robot HAL. (premise)
4. HAL repairs all robots that do not repair themselves. (premise)
5. HAL repairs no other robots. (premise)
That this set of assumptions is contradictory is proved, in effect, by the valid argument of the paradox that leads to a contradiction. We have:
6. No robot, other than HAL, repairs robots other than itself. (From 4.)
7. HAL does not repair himself. (from 4 and 5)
8. HAL does repair himself. (from 2. and 6.)
Conclusions 7. and 8. Contradict.
Thus one cannot hold all of assumptions 1 to 5 without contradiction. Since there is no fallacy in the inferences, we escape the paradox by treating is as a reductio and denying some of the premises.
We could just deny 1, for example, and the paradox would evaporate since there are no robots to be involved in contradictions. However, in seeking our escape, it is customary to deny the least possible and to seek out those parts of the premises most directly responsible for the contradiction. Clearly, assumptions 1-3 are of such a general character that we go too far in denying them.
The trouble lies in 4 and 5. Each of 4 and 5 by themselves produces no problem. It is the conjunction of 4 and 5. that leads to the contradiction. We escape the paradox by denying this conjunction. There can be no robot HAL satisfying both 4 and 5.
The paradox of the asymmetric mirror can be baffling since the contradictory assumptions upon which it is based are hard to delineate--until you see them!
Here is the argument of the paradox made explicit:
1. A mirror image switches left and right.
(premise)
2. A mirror image does not switch up and down. (premise)
3. A mirror is symmetric and treats left-right and up-down the same.
(premise)
4. A mirror image switches up and down. (from 1. and 3.)
5. A mirror image does not switch left and right. (from 2. and 3.)
There are two contradictions arrived at in this argument. 1 contradicts 5. 2 contradicts 4.
The origin of these contradictions lies in premise 1. It contradicts the other premises 2 and 3, which are true of ordinary mirrors. Mirrors do not switch left and right. Rather, they switch back and front, as shown in the figure.
As we approach the mirror, we have the red figure first; and then the blue figure; and then the surface of the mirror. This order reverses in the mirror image. As we follow the images deeper into the mirror world, we have the blue figure first and then the red figure. Back and front have been switched and in a way that is compatible with the mirror treating left-right and up-down in the same way.
If we appropriately adjust the premises in the argument, we no longer arrive at a contradiction:
0. A mirror switches back and front.
1. A mirror image does not switch left and right.
(premise)
2. A mirror image does not switch up and down. (premise)
3. A mirror is symmetric and treats left-right and up-down the same.
(premise)
4. A mirror image does not switch up and down. (from
1. and 3.)
5. A mirror image does not switch left and right. (from 2. and 3.)
In the amended argument, the adjusted conclusions 4 and 5 simply repeat premises 1 and 2, without contradiction.
The lingering puzzle, however, is why we so routinely believe that mirrors switch left and right, when they do not. That derives from the way that we judge how a mirror image is altered. We try to imagine ourselves in the mirror and then check for differences between our imagined figure and the mirror image. The most noticeable fact about a mirror image of ourselves is that the image faces out towards us, while we face towards the mirror. We seek to imagine a version of ourselves in the mirror that also faces out. We will compare it with the mirror image.
To do this, since humans are symmetrical near enough about a vertical plane, we rotate ourselves in imagination around an axis passing from our head to our feet. We then compare that rotated figure with the mirror image and note that the two differ by a left-right flip but not an up-down flip.
There is an asymmetry in this result. But it does not derive from the mirror. Rather we introduce it by rotating ourselves in imagination about the vertical axis and not a horizontal axis. Had we instead performed the rotating in imagination about a horizontal axis, we would have concluded that the mirror flips up and down, but not right and left.
Paradoxes that depend on validly deriving contradictions are close to the argument form reductio ad absurdum. In it, we posit some proposition for testing. We then infer a contradiction from it and thus conclude that the original proposition must be false.
Since many paradoxes end in a contradiction, many of them can be comfortably reconfigured as a reductio. All that is needed is to add an extra step to the argument in the paradox. We diagnose the origin of the contradiction as due to one or more premises, which are negated.
The paradox of HAL the robot leads us by reductio to negate the assumption that a robot repairs exactly those robots who do not repair themselves.
The asymmetric mirror leads us by reductio to negate the assumption that an ordinary mirror reflects left and right.
The irresistible force paradox leads us by reductio to negate the assumption that we can have both an irresistible force and an immovable object.
All paradoxes fall into one of the two categories above:
• an apparent absurdity or
• reasoning that is fallacious or proceeds from a false premise.
Paradoxes can be malleable. Depending on just how we decide to treat them, we may find that we convert one case into the other. This can happen in both directions.
The accelerating spaceship paradox was diagnosed above as a case of a merely apparent absurdity. If we add the assumption that an object like a spaceship must always be somewhere in space, then we have promoted the paradox into one with a real contradiction.
The chicken and the egg paradox may similarly be promoted into a paradox with a real contradiction by adding the assumption of a finite past to the lineage of chickens and eggs.
The reverse process can also happen. A paradox with a validly derived contradiction may be demoted to a mere apparent absurdity by eliminating offending assumptions.
This is illustrated in two examples of the last section. Both the accelerating spaceship paradox and the chicken and egg paradox can be demoted back to paradoxes with only apparent absurdity by removing the assumptions just added.
Summary: How to Diagnose, Treat and Cure a Paradox
The ONLY options are:
(tag: "apparent")
Determine that the absurdity of the paradox is only apparent.
(tag: contradictory assumptions)
Expose the contradictory assumptions employed and
abandon or modify sufficient of them to eliminate the contradiction.
(tag: fallacy)
Expose a fallacy in the reasoning.
To think about for the next class:
Is this last recipe for curing paradoxes exhaustive. Are all paradoxes dependent on an apparent absurdity, contradictory assumptions or fallacies of reasoning? Are there other cases?
June 3, 2021.
December 19, 2022.
Copyright, John D. Norton