
https://commons.wikimedia.org/wiki/File:Dice_-_1-2-4-5-6.jpg
| HPS 0628 | Paradox | |
Back to doc list
Problems for Probability:
the Principle of Indifference
John D. Norton
Department of History and Philosophy of Science
University of Pittsburgh
http://www.pitt.edu/~jdnorton
Linked document: Bertrand's Geometrical Paradoxes: Proofs
How are we to assign probabilities to outcomes? So far, the probabilistic systems we have considered arise within mechanical randomizers, such as coin tosses and die rolls. There the physical properties of the randomizers are so set up that the probabilities assigned to the various outcomes are unambiguous. We make sure that our dice a perfect cubes and rolled with vigor, so each outcome has an equal probability.

https://commons.wikimedia.org/wiki/File:Dice_-_1-2-4-5-6.jpg
How are we to treat systems in which these careful provisions are not in place? What is the probability that the stock market goes up tomorrow versus goes down? What is the probability that there will be a snowstorm on January 1 next year? What is the probability that there is life on some recently discovered, distant planet?
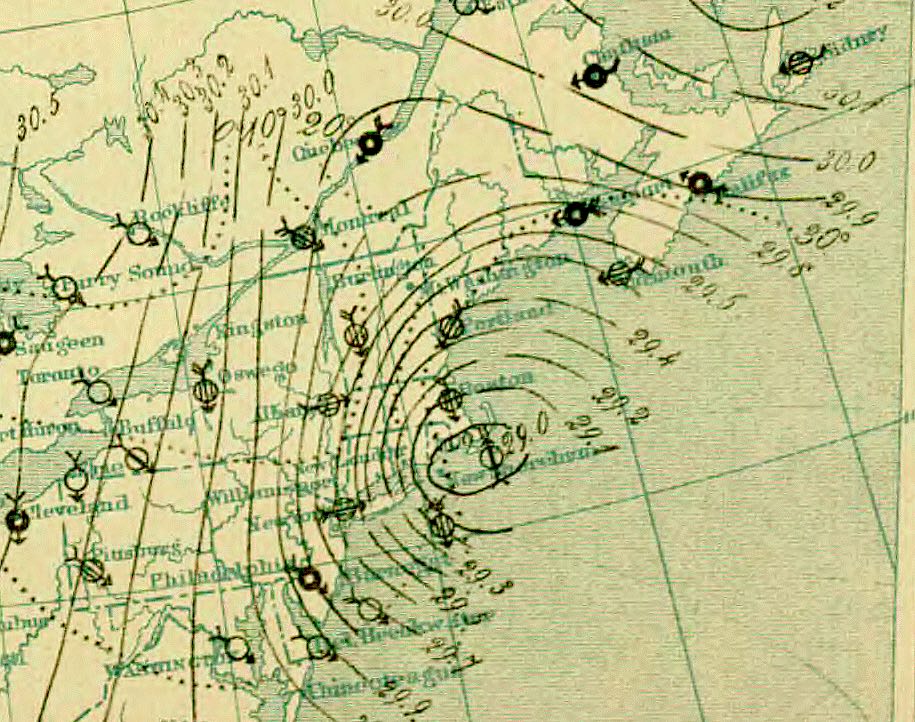
https://commons.wikimedia.org/wiki/File:10_PM_March_12_surface_analysis_of_Great_Blizzard_of_1888.png
The principle of indifference offers assistance that can be applied in many contexts. We might take the case of a coin toss to direct us. In it, we have a good basis in the mechanics of coin tossing to assign equal probability to heads and tails. The mechanism treats each equally and gives us no reason to favor one over the other.


To migrate to the principle of indifference, we extract this "no reason to favor one over the other" and use it by itself. The principle of indifference generalizes this extracted idea to all cases. "No reason to favor" becomes "equal probability." This apparently innocent principle rapidly leads to paradoxes, as we shall now see.
An early and still definite treatment of the principle of indifference is in Chapter 4, "The Principle of Indifference," of Keynes' A Treatise on Probability (London: MacMillan, 1921). In this chapter, Keynes names the principle. He judges it a better name that the earlier "principle of non-sufficient reason."

Here is his statement of the principle (his emphasis, p. 42):
"The Principle of Indifference asserts that if there is no known reason for predicating of our subject one rather than another of several alternatives, then relatively to such knowledge the assertions of each of these alternatives have an equal probability. Thus equal probabilities must be assigned to each of several arguments, if there is an absence of positive ground for assigning unequal ones."
This formulation of the principle is immediately followed by an ominous:
"This rule, as it stands, may lead to paradoxical and even contradictory conclusions..."
Keynes provides a series of illustrations of the
problems that come with the principle. The first and simplest concerns a
book that we have not yet seen and we are unsure of
the color of its cover.
Might it be red?
Since we know nothing of the color of the book, we have as much reason to
expect red as not-red. We have no reason to prefer
one over the other. It follows from the principle that we must assign an
equal probability to both cases. Since those two cases exhaust all the
possibilities, they must sum to one. That is, each must be probability one
half:
Probability (red) = 1/2
Now we ask, might the color be black? We have no reason to prefer black over non-black. By the same reasoning, we again arrive at a probability of one half.
Probability (black) = 1/2
Again, we ask might the book be blue? A similar analysis yields a probability of one half.

Probability (blue) = 1/2
Combining these three probabilities, we have:
 Probability = 1/2 |
 Probability = 1/2 |
 Probability = 1/2 |
Since these colors are mutually exclusive and also mutually exclusive of other colors, we have
P(red) + P(black) + P(blue) + P(some other
color)
≥ P(red) + P(black) + P(blue)
= 1/2 + 1/2 + 1/2 = 3/2
We immediately have a contradiction with normalization of the probability distribution to one. For, as we were reminded in the probability refresher, the total outcome space has the maximum probability one. These three probabilities already sum to greater than one.
This illustration is one of
many that populate the literature on the principle of
indifference. They are essentially the same paradox, but dressed up in
different specifics.
There is a solution that, initially, appears as if it will resolve the paradox. It is that we should select the finest partition of the outcome space, that is the one with the most specific outcomes, and apply indifference just to the outcomes of the finest partition.
Something like it is familiar from the analysis of coin tosses and related problems. For example, assume that there are two coins on display.

What is the probability for each of the three possibilities: no heads, one head, two heads. Since we have no reason to prefer one over another, the principle of indifference direct us to assign equal probability to each, that is, a probability of 1/3rd to each:
Probability = 1/3 |
 Probability = 1/3 |

 Probability = 1/3 |
Anyone who has a familiarity with coin tossing problems will immediately want to correct this list of possibilities.
No heads, one head, two heads
It is not the finest partition of the outcome space. We learned repeatedly that we need to break up the second outcome into two outcomes, so that the full space has four outcomes:
No heads,
head on first coin and tail on second,
tail on first coin and head on second,
heads of both coins
Assigning equal probability to each of these four outcomes gives us:
  Probability = 1/4 |
  Probability = 1/4 |
  Probability = 1/4 |

 Probability = 1/4 |
The escape proposed is that the paradoxes of indifference disappear if we proceed to the finest partition and apply the principle of indifference there only.
It may seem that this restriction to the finest partition resolves the paradoxes. However that is hasty. First, we should note that the familiar coin tossing case suggests but not does require the finer distribution of probabilities of 1/4 for each case.
The reason is that, in the coin tossing case, we are told antecedently, as part of the initiation of the problem, that each coin is tossed fairly and that the tosses are independent. Those physical conditions determine the result that the probability of the four familiar outcomes are equal.


We have no corresponding physical background in the present case. All we are told is that there are two coins on display:

The conditions under which they come to be displayed are not specified. We have no details of the physical process that put them in the frame. Perhaps these are rare coins in a coin collector's display. Then it is very likely that the collector wants to display both sides of the coin, so that one head-one tail is the probability one case.
it does seem rash to assume that the world will always present us pairs of coins just as if they had a history akin to that of two tossed coins. This does not mean that the principle of indifference has been refuted. Rather it underscores just how different are the directions of the principle from the more familiar analyses of coin tosses and the like.
What does present insoluble problems for this "finest partition" escape is that there are many cases in which there is no finest partition; or in which there are multiple candidates that yield contradictory results.
Consider again Keynes' case of the book covers. There is no finest partition. The colors form a continuous spectrum. It spans light with wavelengths of roughly 400 to 700 nanometers (nm).
https://commons.wikimedia.org
/wiki/File:Linear_visible_spectrum.svg
There is no finest division
of these colors. Any small interval of colors can be divided into smaller
intervals and then still smaller intervals without end. The range of 400
to 440 can be divided into 400 to 420 and 420 to 440; and then these into
400 to 410, 410 to 420, 420 to 430 and 430 to 440; and so on indefinitely.
Perhaps, one might imagine, that there is still a way to save something like the idea of the finest partition in these cases. Perhaps we do not assign probabilities indifferently to the individual cases, but to equal intervals of wavelengths, no matter how small the intervals may be. This would correspond to a uniform distribution over the wavelengths. We might assign equal probabilities to steps of size ten:
P(400 to 410nm) = P(410 to 420nm) = P(420 to 430nm) = ... = P(690-700nm)
If we make this uniform assignment, it will be compatible with any other uniform assignment that assigns the same probability to equal intervals. Thus it entails
P(400 to 500nm) = P(500 to 600nm) = P(600 to 700nm)
Tempting as this proposal may be, it fails since there is no reason to distribute our indifferences uniformly over the wavelengths of light. We might equally represent the spectrum of colors using frequencies, measured in TeraHertz, THz.
https://commons.wikimedia.org/wiki/File:Inverse_visible_spectrum.svg
The range of frequencies of visible light is roughly 430 THz to 750 THz.
The problem is that a uniform distribution over the wavelengths is not uniform over the frequencies; and a uniform distribution over the frequencies is not uniform over the wavelengths.
This failure of uniformity follows from the relationship between wavelength and frequency:
300,000 = wavelength in nm x frequency in Thz
To see how this failure arises, consider equal intervals of wavelength and how they translate into unequal intervals of frequencies.
| Wavelengths (nm) | Wavelength intervals (nm) | Frequencies (THz) | Frequency intervals (THz) |
| 400 to 500 | 100 | 600 to 750 | 150 |
| 500 to 600 | 100 | 500 to 600 | 100 |
| 600 to 700 | 100 | 430 to 500 | 70 |
To see the contradiction,
uniformity of probability over wavelengths leads us to require
P(400 to 500 nm) = P(600 to 700 nm)
which is equivalent to requiring
P(600 to 750 THz) = P(430 to 500 THz)
However the interval 600 to 750 THz is of size 150THz, which is
over twice the interval of 430 to 500 THz of size 70 THz. Equality of
probability over equal frequency intervals would lead us to require that
P(600 to 750 THz) > 2 x P(430 to 500 THz)
In the reversed case, we start by considering equal
intervals of frequency. They then correspond to unequal intervals
of wavelength. The table uses a slightly
adjusted range of frequencies for arithmetic simplicity.
| Frequencies (THz) | Frequency intervals (THz) | Wavelengths (nm) | Wavelength intervals (nm) |
| 420 to 530 | 110 | 566 to 715 | 149 |
| 530 to 640 | 110 | 469 to 566 | 97 |
| 640 to 750 | 110 | 400 to 469 | 69 |
This outcome is a paradox with a true contradiction. For repeated application of principle of indifference leads us to conclude two results that contradict:
Probability is uniform over wavelength.
Probability is uniform over frequency.
This mode of failure of the principle of indifference has appeared frequently in the literature in different guises. What they commonly share is that there are two variables used to describe some system, where one is related inversely to the other.
Keynes (p. 45) example of this type concerns the specific volume and the specific density of some substance. One is the reciprocal of the other. Hence we have:
specific volume x specific density = 1
Von Mises has a celebrated example of a mixture of wine and water. His two variables are the ratio of wine to water; and the ratio of water to wine. Once again we have:
ratio wine to water x ratio water to wine = 1
In both cases, using the same reasoning as with the light spectrum, we conclude that uniformity over one variable precludes uniformity over the other. However the principle of indifference requires us to distribute probabilities uniformly over both.
What is striking in these last examples is how each depends on a pair of variables that apply to the same system. The pair has been carefully chosen so that we might plausibly be indifferent over either of them. In all the examples above, however, the variables pertain to continuous magnitudes, like wavelength and frequency, or specific volume and specific density. Is it possible to have a similar problem for the principle of indifference in a system of finitely many components only? The diamond checkerboard is such a case.
One square has been chosen in the diamond checkerboard shown below. We do not know how the square has been chosen. We will use the principle of indifference to form our probabilities for the location of the chosen square.
The open question is how the indifference is to be applied. An obvious candidate is indifference over each of the 13 individual squares. Then each square ends up with a probability of 1/13. Or we might be indifferent over whether the chosen square is dark or light. Then the dark squares accrue probability 1/2 and the light squares also accrue probability 1/2.
If, however, we seek a pair of indifferences like those over the pairs of variable in the last section, there are several ways to do it. We might be indifferent over the diagonal rows. One way of implementing this indifference is shown below. Each of the five diagonal rows is then accorded a probability of 1/5.
We could also apply indifference over the diagonal rows oriented in the other direction. Once again each diagonal row is accorded a probability of 1/5.
The important question is whether these two different applications of indifference are compatible. That is, can we find a probability distribution over the individual squares the conforms with both? Yes we can. It is shown below.
If we sum the probabilities show along the diagonals, we recover a probability of 1/5 for all of the diagonals. The two applications of indifference are consistent.
That is how things proceed when there are no problems. A different pair of invariances, however, leads to contradictions. We might be indifferent over the horizontal rows; or over the vertical columns. Because of the symmetry of the diamond, there is no reason to prefer one of the horizontal or vertical over the other.
Here is what happens if we are indifferent over the horizontal rows:
For each row, there is a probability of 1/5 that the row contains the selected square. Here is what happens if we are indifferent over the vertical columns:
The resulting probabilities from the two cases are NOT compatible. To get a sense of this, imagine that we fill in the probabilities of the individual squares for the first case of indifference over the horizontal rows. If we distribute the probabilities uniformly within the rows, we find:
It is immediately clear that these probabilities are incompatible with those derived from indifference over the vertical columns. The central column, for example, in this vertical case, should have a probability of 1/5. In the distribution derived from indifference over the horizontal rows the central vertical column has a probability
1/5 + 1/15 +1/25 + 1/15 + 1/5 = 43/75 > 1/2
This last distribution of probabilities over the individual squares is just one of many that would be compatible with indifference over the horizontal rows. We can see fairly easily that no other distribution will solve the problem. Any distribution of probability over the squares that is compatible with indifference over the horizontal rows will be incompatible with indifference over the vertical columns. For indifference over the horizontal rows forces the probabilities assigned to the individual top and individual bottom squares to be each 1/5, as shown below. However that means that the probability assigned to the central vertical column must be at least 1/5 + 1/5 = 2/5.
The corresponding incompatibility with indifference over the horizontal rows arises if we start with indifference over the vertical columns.
In this case of the diamond checkerboard, there are equally good reasons to be indifferent over the horizontal rows and the vertical columns. However indifferences over both produce contradictions.
A large collection of problems for the principle of induction are associated with "geometrical probabilities" (as identified by Keynes, pp. 47-48). They have the same general structure as the light spectrum case, but are now implemented in a geometrical setting.
One of the simplest of these geometrical paradoxes has been developed in the budget of paradoxes as "Lost in the Desert." Stripped of the lost camper narrative, the paradox concerned the probability of a random point being in the inner circle or in the outer ring of the figure:
If we are indifferent over the distance from the center, then the probability that the point is in the inner circle is the same as the probability that it is in the outer ring. For the range of distances from the center in the inner circle (0 to 1, say) is the same as the range of distances from the center spanned by the outer ring (1 to 2, say).
If we are indifferent over areas, then the probability that the point is in the inner circle is one third the probability that it is in the outer ring, for the outer ring has three times the area.
This is the simplest of the geometric style paradoxes derived from the principle of indifference. Best known among many more examples are those presented by Joseph Bertrand in his 1907 treatise on the probability calculus.

Among Bertrand's examples, the best known is the problem of the chord in a circle. Bertrand considers a circle with an equilateral triangle inscribed inside.
He then considers an indifferently chosen chord of the circle and asks for the probability that its length is greater than the side of the equilateral triangle. Bertrand arrives at different answers according to how indifference is applied. Here are his three cases and the results he achieves:
| Probability = 1/3 Indifference over the angles of chords drawn from a point at the apex of the triangle. |
Probability = 1/2 Indifference over chords drawn perpendicular to a radius of the circle. |
probability=1/4 Indifference over the position of the center of all chords drawn in the circle enclosed by the triangle. (Chords with center points in the inner circle are longer than the side of the triangle.) |
Bertrand's Geometrical Paradoxes: Proofs
These elaborate geometrical paradoxes are quite entertaining. Bertrand's ingenuity is displayed through his finding a case in which we have all three of the simplest probabilities--1/2, 1/3, 1/4--applied in the same case. However, they do not reveal any deeper foundational problems than have already been raised by the simpler version of "lost in the desert" and, before that, indifference over colors.
Here is Bertrand's original text:

The highlighted text gives Bertrand's assessment:
"Entre ces trois résponses,quelle est la véritable? Aucune des trois n'est fausse, aucune n'est exacte, la question est mal posée."
"Among these three answers, which is the correct one? None of the three is wrong, none is correct, the question is badly posed."
The paradoxes of indifference have been prominent in the literature on probability and have a long history. There have been many solutions offered for them. Some (following Keynes) seek to restrict the situations in which indifferences can be applied. Others seek to escape the paradoxes by relaxing or generalizing how we treat uncertainties formally. In my view, this second approach is correct.
Here is my version of this escape from the paradox.
Keynes' canonical statement of principle of indifference has two components in it. He writes, as quoted above:
"The Principle of Indifference asserts that if there is no known reason for predicating of our subject one rather than another of several alternatives, then relatively to such knowledge the assertions of each of these alternatives have an equal probability. Thus equal probabilities must be assigned to each of several arguments, if there is an absence of positive ground for assigning unequal ones."
The two components are indicated by boldface.
The first is a principle or rationality.
If you have no reason to prefer one possibility over another, you should not prefer one over the other.
This is about as benign a truism of rationality as I can conceive. It goes to the heart of rationality. Our beliefs and approaches should be governed by reasons; and if reasons are powerless to distinguish cases, then the cases should be treated alike.
There is considerable vagueness in this formulation. What does it mean to "treat" in "treated alike"? Here we can fill in many possibilities. There are two extremes
One extreme is that our concern is our belief states. We should have the same belief in the two possibilities.
Another is a belief independent notion of evidential support. Then the principle becomes a principle of evidence: if the evidence cannot distinguish two cases, then both are equally well supported.
This first component of Keynes' statement is not troublesome. The trouble comes with the second component. How are we to represent belief states; or the strengths of evidential support; or whatever might be intermediate between them? Keynes' second component prejudges the situation and simply presumes that probabilities will always apply.
The real import of the paradoxes of indifference is that they show this second presumption is too hasty. We can contrive circumstances in which probabilities simply fail to accommodate the benign principle of rationality above.
The most extreme case of indifference arises when we are indifferent over all contingent outcomes. We can deduce from the principle of indifference the formal properties an appropriate representation of complete ignorance states or completely neutral evidential support. In short:
Completely neutral support: All contingent outcomes accrue the same support.
In the case of discrete outcome spaces, such as the two coin tosses, every contingent outcome will be attributed the same indifference or ignorance value "I." Writing in terms of inductive support on the evidence, we have:
support(no heads) = I
support(first heads then tails) = I
support (first tails then heads) = I
support (one head only)
= support( first heads then
tails OR first tails then heads) = I
support (two heads) = I
if we are completely ignorant of the circumstances that lead to the coin arrangement or if the evidence completely fails to distinguish any arrangement, then we must treat all contingent outcomes alike.
This last ignorance or indifference distribution violates the additivity of a probability measure:
support (one head only)
= support( first heads then
tails OR first tail then heads)
=
support(first heads then tails) = support (first tails then heads)
support(
 or
or 
 )
)
= support(
 ) = support(
) = support(
 )
)
This failure of additivity seems to me to be the key result.
In the case of a continuous outcome space, such as the color spectrum, all intervals of wavelength would be assigned the same support:
support (wavelength in 0 to 1) = support
(wavelength in 1 to 2)
= support (wavelength in 2 to 3) = ... = I
= support (wavelength in 0 to 2) = support (wavelength in 2 to 4)
= support (wavelength in 4 to 6) = ... = I
= support (wavelength in 0 to 1) = support (wavelength in 1 to ∞) = I
= support (wavelength in 0 to 2) = support (wavelength in 2 to ∞) = I
etc.
This distribution is illustrated here. Each of the intervals marked out by the bars are assigned the same support I:
The states of completely neutral support or complete ignorance are largely determined by two invariances that are implicit in the paradoxes of indifference.
The first pertains to what happens when we refine or coarsen outcomes:
I. Invariance under redescription: Completely neutral support is unchanged if we refine or coarsen our description of the outcome space.
"Refinement" means replacing some outcome by its disjunctive parts. For example, in the case of the two coins, we would replace
"one head only"
by
"heads first then tails OR tails first then heads."
Thus, if the principle of indifference indicates that support for no heads is the same as for one head, then that equality is not altered when we note that "no heads" has two disjunctive parts.
support(no )
= support(one
)
= support(one )
)
= support(
 or
or 
 )
)
The second invariance pertains to negation.
II. Invariance under negation: In completely neutral support, the support for an outcome is unaltered if we replace it by its negation.
The quick way to see this is to imagine some contingent proposition "A" about which we know nothing or for which there is no evidence. How does our state of belief or the level of support alter if we replace A with "not-A"? Since we have complete neutrality, it should not change.
This second invariance is illustrated with the color spectrum. Consider the possibility that some electromagnetic wave has a completely unknown wavelength and frequency. To proceed, we will measure the wavelength in units of √300,000nm = 548nm; and frequency in units of √300,000THz = 548THz. The reason is that then the relationship between them becomes very simple:
wavelength x frequency = 1
Consider the support accrued to the two wavelength intervals,
0 to 1 and 1 to ∞.
Each is the negation of the other.
It is tempting initially to assign greater support to the infinite interval 1 to ∞, since it is infinite. That possibility proves unworkable. If we redescribe the two outcomes in terms of frequency, which are the finite and which are the infinite intervals switch:
wavelength (0 to 1) = frequency (1 to ∞)
wavelength (1 to ∞) = frequency (0 to 1)
The figure shows which intervals match physically in the two scales of wavelength and frequency:
If the infinity of an interval means it should have greater support, then we arrive at a contradiction. We would infer from it:
Greater support for wavelength (1 to ∞), since it
is an infinite interval.
Greater support for wavelength (0 to 1), since it corresponds to an
infinite interval of frequency.
To escape the contradiction, we assign equal support to all these four intervals:
wavelength (0 to 1), wavelength (1 to ∞), frequency (0 to 1), frequency (1 to ∞)
These equalities implement invariance under negation. A negation takes us from the interval wavelength (0 to 1) to wavelength (1 to ∞); and from frequency (0 to 1) to frequency (1 to ∞).
Another approach in this tradition is worth mentioning. In the approach above, an outcome can have the same support as its disjunctive parts. In the two coin example, an outcome "one head" can have the same support as "first heads then tails" and as "first tails then heads."
For some, this equality is intolerable. It can be escaped if we deny that the support for mutually exclusive outcomes can be compared. We simply refuse to judge whether:
"First heads then tails"
is more strongly supported than "first tails then heads."

 ?>?
?>?

"First heads then tails" is equally supported as "first tails then heads."

 ?=?
?=?

"First heads then tails" is less strongly supported than "first tails then
heads."

 ?<?
?<?

We withhold judgment and assert
none of these.

 ??
?? 

Then it is possible to avoid the paradoxes. We can say, for example, that:
"One head in two tosses"
is more strongly supported than "first tails then heads."
1 >
>

"One head in two tosses" is more strongly supported than "first heads then
tails."
1 >
>

However the few comparisons allowed are insufficient
to enable a paradox of indifference to be set up.
The long-standing paradoxes of indifference have an interesting history. They arose as a by-product of the expansion of the theory of probability from games of chance to other contexts.
When the theory was developed in the sixteenth and seventeenth century by Cardano and Huygens as a theory that counted chances, their primary concern was the analysis of games of chance. These games, by design, were developed around an outcome space whose individual outcomes had the same chance. All possible pairs of outcomes on two dice rolls, for example, have the same probability.
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
In this most hospitable environment, the comparable likelihood of different outcomes could be determined simply by counting cases. Rolling a two with two dice could happen in only one way
Rolling a seven, however, could happen in six ways.
,
,
,
,
,
It followed that the seven was six times as likely as the two. It was easy then and remains easy today to deal with simple gambling problems merely by counting cases.
The notion of probability was a derived notion. That is, the idea of the equally likely case was fundamental, the starting point. Once these cases were secured, probability could then be defined as a simple ratio:
probability = (number of favorable case) / (number of all cases)
Thus the probability of a seven was (6 favorable cases) / (36 cases in all) = 1/6.
This was the conception of probability employed by Laplace in his 1814 "Essai philosophique sur les probabilités." Following many before him, he was, in his essay, seeking to extend the reach of probabilistic thinking to broader matters. His introductory examples included discussion of the motion of comets and conjectures on the motion of molecules. He then sought an extension of the gambler's notion of probability:
"The theory of chance consists in reducing all the events of the same kind to a certain number of cases equally possible, that is to say, to such as we may be equally undecided about in regard to their existence, and in determining the number of cases favorable to the event whose probability is sought. The ratio of this number to that of all the cases possible is the measure of this probability, which is thus simply a fraction whose numerator is the number of favorable cases and whose denominator is the number of all the cases possible."
This came to be known as the "classical interpretation of probability."
The difficulty with this conception is that the more removed we are from the context of games of chance, the harder it becomes to effect the reduction to equally likely cases. The paradoxes of indifference arise from efforts to determine if Laplace's definition is viable.
The descent to paradox is already visible in Laplace's definition. He writes of us being "equally undecided" as the criterion for distinguishing the cases whose number will be used to compute the probability.
In games of chance, we have (as noted above) something stronger than indecision. We have positive, antecedent physical reasons for expecting the base cases to be equally likely. We toss fair coins in such a way as to ensure it.


Now we are simply told that we have two coins on display and are given no history of how they came to be displayed. When we are asked which faces are uppermost, we are faced with a problem different from that of the tossed coins.

Can we be confident that the same methods that succeeded with games of chance will succeed with the new problem? Work in century following Laplace's essay explored just this question. Keynes asked, what color are we to expect for a book before we see it?



These explorations found that Laplace's condition of our being "equally undecided" could be used to arrive at contradictory probability assignments. They are the paradoxes of indifference.
The solution to the paradoxes of indifference above is to allow that some cases of indefiniteness cannot be represented by the additive measures of probability theory. Is this too severe a response? Should we be ready to abandon probabilities?
The solution above considers two options: a
non-probabilistic representation of indefiniteness or abandoning any
comparison of belief or strengths of support for mutually exclusive
outcomes. Which is preferable?
August 16, December 1, 2021. April 13, 2023. December 30, 2024.
Link to new page with proofs of Bertrand's paradox added January 31, 2025.
Copyright, John D. Norton