

Next: Finite cable
Up: Steady state and boundary
Previous: Steady state and boundary
In this case, we assume that at
x=0 the voltage is clamped to V=V0. The boundedness of the
voltage as 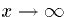 means that we must take
means that we must take
| 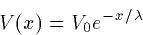 |
(13) |
It is now clear why 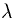 is called a space-constant, it
determines the voltage attenuation with distance.
is called a space-constant, it
determines the voltage attenuation with distance.
Alternatively, we could demand that the current at x=0 be specified
as I0. From (14) we see that
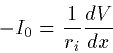
and since 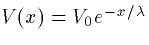 we get
we get
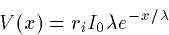
The input resistance is the ratio of V(0)/I0 is thus
| 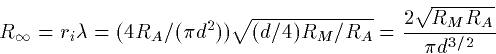 |
(14) |
The input conductance for the semi-infinite cable is thus
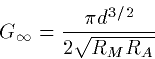
Note: It is often convenient to introduce the dimensionless
space variable, 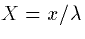 and the electrotonic length of the
cable,
and the electrotonic length of the
cable, 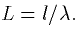 This gets rid of all the divisions by
This gets rid of all the divisions by 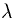 in the exponentials and hyperbolic functions.
in the exponentials and hyperbolic functions.
G. Bard Ermentrout
1/10/1998
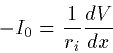
![]()
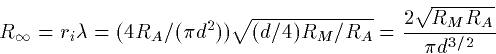
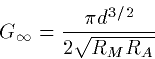
![]() and the electrotonic length of the
cable,
and the electrotonic length of the
cable, ![]() This gets rid of all the divisions by
This gets rid of all the divisions by ![]() in the exponentials and hyperbolic functions.
in the exponentials and hyperbolic functions.