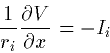

Next: Steady state and boundary
Up: Passive cell models
Previous: Running the simulation
Information flows in the nervous system from the soma to the axon and
then to the dendrites. In most models, the dendrites are regarded as
being passive electrical cables. In this section, the cable equation
is derived, steady state cable properties are studied and total input
resistance of a cell is defined.
Figure 2:
Cable broken up into discrete segments
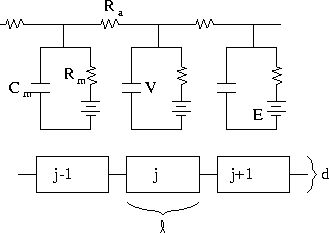 |
We will model the cable as a continuous piece of membrane that
consists of a simple RC circuit coupled with an axial resistance that
is determined by the properties of the axoplasm. Figure 2
shows a piece of a cable broken into small parts. From this figure,
we obtain the following equations
| 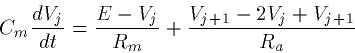 |
(7) |
We have introduced a new quantity, Ra which is the axial
resistance. This as you would guess depends on the geometry of the
cable, in this case, the diameter, d and the length, 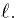 As
with the membrane resistance, there is also a material constant, RA
associated with any given cable. This is measured in
As
with the membrane resistance, there is also a material constant, RA
associated with any given cable. This is measured in 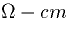 .A typical value is
.A typical value is 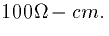 As
anyone who has ever put a stereo will attest, the resistance along a
cable is proportional to its length and inversely proportional to the
cross-sectional area (the fatter the cable, the less resistance) thus
we have the following (using our definitions above)
As
anyone who has ever put a stereo will attest, the resistance along a
cable is proportional to its length and inversely proportional to the
cross-sectional area (the fatter the cable, the less resistance) thus
we have the following (using our definitions above)
We plug these into (7), let 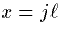 define distance along
the cable, and then take the limit as
define distance along
the cable, and then take the limit as 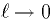 to obtain the
continuum equation for the cable:
to obtain the
continuum equation for the cable:
| 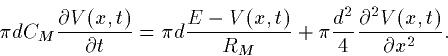 |
(8) |
We multiply both sides by 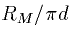 and obtain the following
equation:
and obtain the following
equation:
| 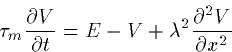 |
(9) |
where 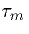 is the time constant RM CM and
is the time constant RM CM and
| 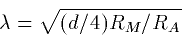 |
(10) |
is called the space constant of the cable. The space constant depends
on the diameter while the time constant depends only on the material
constants. Using 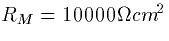 and
and 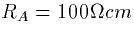 we
obtain
we
obtain
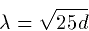
so if the dendrite has a diameter of, say, 10 microns, or 0.001
centimeters, the space constant is 0.07 centimeters or 0.7 mm. The
space constant determines how quickly the potential decays down the
cable.
An alternate derivation is given by Segev in the Book of GENESIS. The
longitudinal current, Ii is given by the following:
| 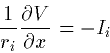 |
(11) |
where ri is the cytoplasmic resistivity as resistance per
unit length along the cable. This is just 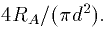


Next: Steady state and boundary
Up: Passive cell models
Previous: Running the simulation
G. Bard Ermentrout
1/10/1998

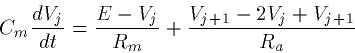
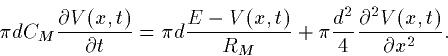
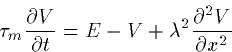
![]()