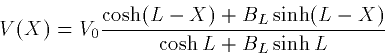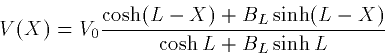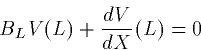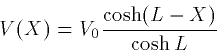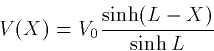

Next: Solving boundary value problems
Up: Steady state and boundary
Previous: Semi-infinite cable
There are a variety of possible end conditions we can apply to the
cable. Among them are the (a) sealed end where no current can
pass and so dV/dx=0, (b) short circuit or open end where
the voltage is clamped to 0, (c) leaky ends which is a mixture
of the two, some current escapes but not an infinite amount. Let's
revert to the dimensionless equations 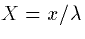 and
and 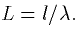 Assume that the voltage at X=0 is V0. Then the general solution
to the steady-state equation is:
Assume that the voltage at X=0 is V0. Then the general solution
to the steady-state equation is:
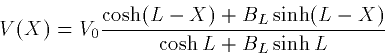
where BL is an arbitrary constant. This general solution is
equivalent to asserting that the boundary condition at X=0 is V0
and that at X=L
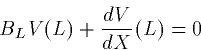
The free parameter, BL is the ratio of the input conductance for
the cable, GL to that of the semi-infinite cable, 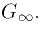 That
is,
That
is, 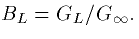
For example, if we want the
sealed end condition at X=L we take BL=0 so that
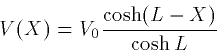
If we want the open end conditions, we take 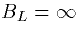 so that
so that
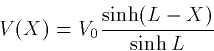
If we choose BL=1 then
V(X) = V0 e-X
which is precisely the solution to the semi-infinite cable.
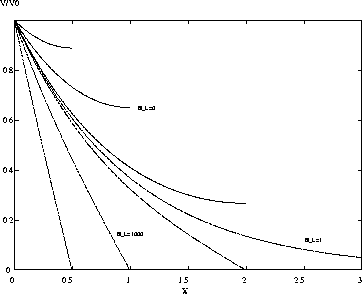
In figure 3 we plot the steady state voltages for a variety
of different cables and at different electronic lengths. These could
be solved analytically, but the plots were in fact generated by using
XPPAUT.
Figure 3:
Steady state voltages for a variety of electrotonic lengths
and for different end conditions
 |


Next: Solving boundary value problems
Up: Steady state and boundary
Previous: Semi-infinite cable
G. Bard Ermentrout
1/10/1998