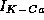Bursting can arise even without bistability in the spike-generating
dynamics. Minimal models for the most widely known endogenous
cellular burster, the Aplysia R-15 neuron, operate in a regime where
the fast dynamics is monostable ([30]).
Suppose the spiking dynamics are as in Figures 4
- 6 , where the onset of
repetitive firing is through a saddle-node-loop bifurcation and there is no
bistability. (Ignore the bistable behavior at high currents.
We are interested in
the low current regime only, where the rest state is more negative
than -30 mV.) The
mechanisms for bursting that depend on one slow variable cannot produce
bursting in this parameter regime since there is no longer a
hysteresis loop.
A model with a single slow variable
interacting with these fast dynamics will, in response to a
steady input, slowly
approach a maintained state of repetitive firing or rest.
The slow transient phase for a depolarizing
input could show increasing or decreasing activity
depending on whether the slow variable provides positive or negative
feedback.
Figure 11a illustrates that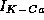 
with slow Ca dynamics
provide a mechanism for adaptation in repetitive firing behavior.
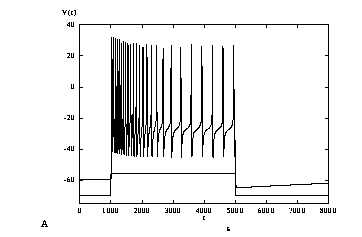
Integrate this and then set gkca=0 and integrate again to see the effects of adaptation. Set gkca to a variety of values between 0 and 2 to see how adaptation is affected. (Hint: If you are using the most recent version of XPP, bind a slider to gkca whose standard value is 1 for this simulation.)
In order to obtain the slow oscillation that underlies parabolic bursting we need yet another slow variable so that there are opposing influences of slow positive (autocatalytic) and slow negative feedback. Thus, suppose that we add a slow inward current to the model. This means that there are two slow variables. As the inward current slowly activates, it causes the membrane to fire repetitively. However, this turns on the slow outward current which then shuts the membrane down. If the threshold for the slow inward current is low enough, then it can start up once again and the process repeats. Thus, a combination of a slow outward current and slow inward current can produce slow oscillations that move the fast dynamics into and out of the repetitively firing regime. The generality of this mechanism for parabolic bursting (also realizable with an inward current that slowly activates and then slowly inactivates, as in [30]) has been described by a number of authors (e.g., [1]).
To illustrate with the Morris-Lecar model (that includes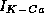 
as
above) we need only add a slow autocatalytic process.
With considerable freedom of choice, we add an additional
slowly activating calcium current:
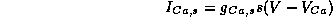
where
For simplicity, we have chosen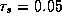 
as a constant and
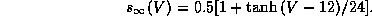
Figure 11b shows the voltage trace of the burst pattern. Note how the interspike interval is relatively longer at the beginning and end of each burst. Figure 11c shows the projection of the two slow gating variables, s and z during a burst. The dashed line represents the boundary between fixed points and oscillation for the fast dynamics when the slow variables are held fixed; it is where the saddle-node-loop bifurcation occurs. Above this line, the fast dynamics are oscillatory and below it, there is a unique stable fixed point.
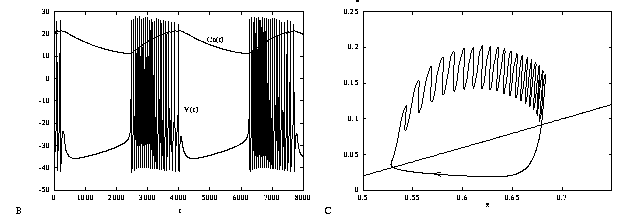
Run this to get the phase-plane picture. Increase the total integration time to 10000 msec and runs again, this time looking at V versus t.
We have shown how modulating the various types of fast dynamics with one or two slow processes leads to simple mechanisms for generating several different types of bursting oscillations. This geometric viewpoint lets us dissect the mechanisms that underlie some complex neuronal bursting dynamics. Other factors can contribute to burst rhythmogenesis including cable properties and spatially non-uniform channel densities, and nonlinear regenerative factors in the calcium handling system (cf. [36]).
