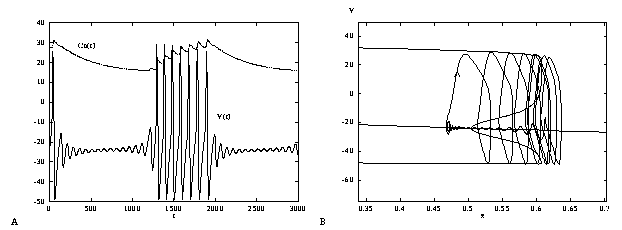
Bursting that differs from the square-wave pattern above can arise from slow modulation of bistable fast dynamics, since bistability can arise in a number of ways. Consider a parameter regime for eqs 4-6 in which the onset of oscillations is via a subcritical Hopf bifurcation, such as shown in Figure 2 and Figure 3. As for the square-wave burster, there is a regime where the spike-generating dynamics is bistable; a limit cycle and a fixed point coexist. However, unlike the bistability shown in Figure 7 , here, the limit cycle ``surrounds'' the fixed point. Figure 10 shows an example of a so-called elliptic burst pattern generated when the fast dynamics of Figures 2 and 3 are coupled with the slow calcium- dependent potassium current used in the previous bursting model (equation 22). Here (Figure 10A) the envelope of the spikes is ``elliptical'' in shape as the amplitude gradually waxes and wanes. The silent phase is characterized by damping and growing oscillations as the trajectory slowly drifts through the Hopf bifurcation of the fast subsystem. This type of activity pattern has been seen in sleep spindles and a cellular model related to it involves this mathemetical mechanism [7] (see also, [36]). As with a square-wave burster, this type of bursting can also have complex dynamics such as quasi-periodic behavior and chaos.

Integrate this equation, look at V versus t , and look at the calcium concentration, Ca . Change the current, I and study what happens.