


Next: Summary
Up: Phase-resetting and Phase-locking
Previous: Phase-response curves
The general behavior of
coupled neural oscillators is very difficult to analyze, however limiting
cases can be treated ([22]). We will describe one
method, the method of averaging, that
has been used successfully to
study the dynamics of two or more neural oscillators that are
weakly coupled
(e.g., Hansel [16] and Ermentrout and Kopell [9]).
In this limit the coupling is sufficiently weak that each oscillator's
trajectory remains close to its intrinsic limit cycle.
The primary effect of the coupling is to perturb the relative
phase between the oscillators much as we described above.
However, since the perturbation per cycle is small (with weak coupling)
the net effect occurs only over many cycles and the per cycle effect
is seen as averaged.
For illustration, we summarize the use of averaging to
describe the phase-locking properties of two identical
Morris-Lecar oscillators when coupled with identical mutually
excitatory synapses. Detailed derivations of the equations can be
found in the above mentioned papers.
We assume that motion of each oscillator along its limit cycle
can be rewritten in terms of a phase variable.
Thus an oscillator's membrane potential
is periodic with period T and follows the
function 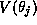 where
where 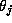 is the phase of the
is the phase of the 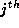 oscillator, j=1,2 and V is the voltage component of the limit
cycle trajectory. In the absence of
coupling the dynamics is given simply as
oscillator, j=1,2 and V is the voltage component of the limit
cycle trajectory. In the absence of
coupling the dynamics is given simply as
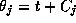 where
where 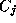 is an arbitrary phase-shift.
Now consider the effect of small coupling.
A brief, weak synaptic current
is an arbitrary phase-shift.
Now consider the effect of small coupling.
A brief, weak synaptic current 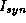 to cell i from
activity in cell j
will cause a phase shift in cell i
to cell i from
activity in cell j
will cause a phase shift in cell i
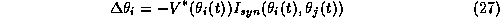
where
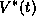 is the infinitesimal phase-response function, and the minus
sign converts excitatory current to positive phase shift.
The synaptic current is given by
is the infinitesimal phase-response function, and the minus
sign converts excitatory current to positive phase shift.
The synaptic current is given by
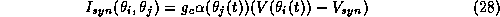
where the postsynaptic gating variable 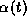 in cell i
is activated by the presynaptic voltage
in cell i
is activated by the presynaptic voltage 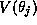 ,
,
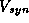 is the reversal potential for the synapse,
and
is the reversal potential for the synapse,
and 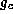 is the strength of the synaptic coupling.
The gating variable
is the strength of the synaptic coupling.
The gating variable 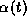 could be represented by
a so-called (event-triggered)
alpha function introduced by Rall (cf. chapter 2 of
this volume). Alternatively, it could obey a voltage-gated
differential equation.
could be represented by
a so-called (event-triggered)
alpha function introduced by Rall (cf. chapter 2 of
this volume). Alternatively, it could obey a voltage-gated
differential equation.
In the method of averaging
we simply ``add up'' all the
phase-shifts due to the synaptic perturbations and average them over
one cycle of the oscillation.
Thus, after averaging, one finds
that the coupled system satisfies:
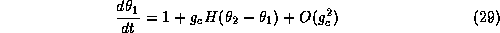
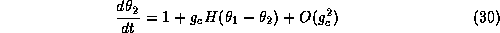
where
H is a T-periodic ``averaged'' interaction function, given by
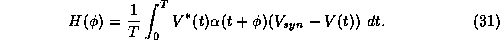
The key to these models is the computation of H
(see [9] and [22]).
In Figure 14A, we show the function 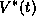 along with the synaptic
gating variable
along with the synaptic
gating variable 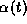 over one cycle for exactly the same
parameters as in Figure 12B. Here
over one cycle for exactly the same
parameters as in Figure 12B. Here 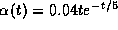 is an
``alpha'' function with a 5 msec time constant. Note the
similarity (except for scale) of the excitatory PRC and the
infinitesimal PRC,
is an
``alpha'' function with a 5 msec time constant. Note the
similarity (except for scale) of the excitatory PRC and the
infinitesimal PRC,  As with the PRC,
As with the PRC,  is mainly
positive showing that the predominant effect of depolarizing perturbations is
to advance the phase or equivalently speed up the oscillator.
In only a very small interval of time can the phase be delayed, and
this is a general property of membranes which become oscillatory through a
saddle-node bifurcation ([8]).
is mainly
positive showing that the predominant effect of depolarizing perturbations is
to advance the phase or equivalently speed up the oscillator.
In only a very small interval of time can the phase be delayed, and
this is a general property of membranes which become oscillatory through a
saddle-node bifurcation ([8]).
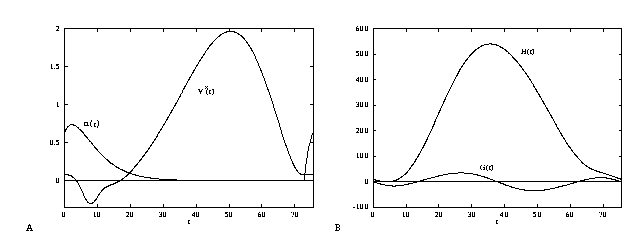
Figure 14
This has been set up so that if you integrate it you will obtain
exactly one cycle with the peak of the oscillation at t=0.
Integrate the equation. Plot the synaptic alpha function, s
as a function of time. Now compute the adjoint as follows. Choose
(nUmerics) (Averaging) (in older versions of XPP, use (Adjoint)
instead of (Averaging)) Choose (New adjoint) and let it compute. Escape
to the main menu and plot V versus t as XPP replaces
the columns with the adjoint. Compare this with the PRC computed earlier. They are close up
to a scaling factor. Now compute the H function. Choose
(nUmerics) (Averaging) (Make H). Type in
s'*(vsyn-v)
when asked for the Coupling for V and type in 0 for the
rest. After a few seconds, the bell will ring and the H will
be computed. Escape to the main menu and plot V which is
replaced by the interaction function. Then plot w which is
replaced by the odd part of the interaction function. Change Vsyn
to make the synapse inhibitory, say -75mv. What are the stable
phaselocked points? Make the synapse very fast by setting alpha=1
Recompute the orbit by choosing (Init conds) (Last) a few times
from the main menu. Compute the adjoint again. Compute the
interaction functions for excitatory Vsyn=0 and inhibitory
Vsyn=-75 synapses and determine the stable phaselocked
states. Change alpha to 20 and do all this again.
Figure 14B shows the function 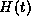 defined in equation (31)
for the alpha function shown in Figure 14A and for
defined in equation (31)
for the alpha function shown in Figure 14A and for 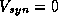 mV. We can
use this function along with equations (29-30) to determine the stable
phase-locked patterns for this coupled system. Let
mV. We can
use this function along with equations (29-30) to determine the stable
phase-locked patterns for this coupled system. Let
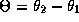 denote the phase difference between the two
oscillators. From equations (29-30)
we see that
denote the phase difference between the two
oscillators. From equations (29-30)
we see that  satisfies:
satisfies:
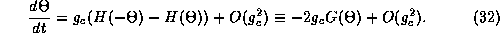
Here 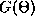 is just the odd part of the function H. Since the
coupling is weak, the higher order terms,
is just the odd part of the function H. Since the
coupling is weak, the higher order terms, 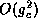 are ignored. Equation
32 is just a first order equation. Phase-locked states are
those for which
are ignored. Equation
32 is just a first order equation. Phase-locked states are
those for which  does not change, that is, they are roots of
the function
does not change, that is, they are roots of
the function 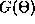 and they are stable fixed points if
and they are stable fixed points if
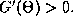 Since any odd periodic function has at least two
zeros,
Since any odd periodic function has at least two
zeros, 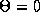 and
and 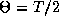 there will always exist
phase-locked states. However, these may not be stable, and there may
be others. Synchronous solutions (
there will always exist
phase-locked states. However, these may not be stable, and there may
be others. Synchronous solutions (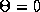 ) imply that both membranes fire
together. Anti-phase solutions (
) imply that both membranes fire
together. Anti-phase solutions (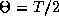 )
are exactly one half cycle apart.
Figure 14b shows the function
)
are exactly one half cycle apart.
Figure 14b shows the function 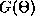 and from
this we see that there are 4 distinct fixed points: (i) the
synchronous
(precisely in-phase) solution, (ii) the anti-phase
solution, and (iii) a pair of phase-shifted solutions at
and from
this we see that there are 4 distinct fixed points: (i) the
synchronous
(precisely in-phase) solution, (ii) the anti-phase
solution, and (iii) a pair of phase-shifted solutions at
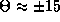 msec. Both the synchronous and anti-phase solutions
are unstable but the phase-shifted solution is stable. Thus, if two of
these oscillators are coupled with weak excitatory coupling and the
parameters chosen as above, they will phase-lock with a phase-shift of
about
msec. Both the synchronous and anti-phase solutions
are unstable but the phase-shifted solution is stable. Thus, if two of
these oscillators are coupled with weak excitatory coupling and the
parameters chosen as above, they will phase-lock with a phase-shift of
about 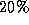 of the period.
Although the classical view is that mutual excitation leads to
perfect synchrony, computations with a variety of
neuronal models suggest that this is not generally the case.
of the period.
Although the classical view is that mutual excitation leads to
perfect synchrony, computations with a variety of
neuronal models suggest that this is not generally the case.
This type of analysis is easily extended to systems where the
oscillators are not exactly identical, when coupling is not symmetric,
and when there are many more oscillators. The behavior of such
phase-models and the forms of the interaction functions, H, are the
topics of current research.


Next: Summary
Up: Phase-resetting and Phase-locking
Previous: Phase-response curves
Bard Ermentrout
Mon Jul 29 17:47:46 EDT 1996
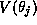 where
where 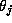 is the phase of the
is the phase of the 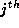 oscillator, j=1,2 and V is the voltage component of the limit
cycle trajectory. In the absence of
coupling the dynamics is given simply as
oscillator, j=1,2 and V is the voltage component of the limit
cycle trajectory. In the absence of
coupling the dynamics is given simply as
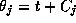 where
where 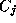 is an arbitrary phase-shift.
Now consider the effect of small coupling.
A brief, weak synaptic current
is an arbitrary phase-shift.
Now consider the effect of small coupling.
A brief, weak synaptic current 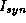 to cell i from
activity in cell j
will cause a phase shift in cell i
to cell i from
activity in cell j
will cause a phase shift in cell i
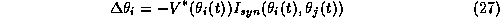
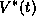 is the infinitesimal phase-response function, and the minus
sign converts excitatory current to positive phase shift.
The synaptic current is given by
is the infinitesimal phase-response function, and the minus
sign converts excitatory current to positive phase shift.
The synaptic current is given by
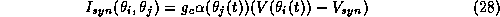
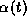 in cell i
is activated by the presynaptic voltage
in cell i
is activated by the presynaptic voltage 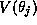 ,
,
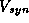 is the reversal potential for the synapse,
and
is the reversal potential for the synapse,
and 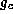 is the strength of the synaptic coupling.
The gating variable
is the strength of the synaptic coupling.
The gating variable 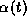 could be represented by
a so-called (event-triggered)
alpha function introduced by Rall (cf. chapter 2 of
this volume). Alternatively, it could obey a voltage-gated
differential equation.
could be represented by
a so-called (event-triggered)
alpha function introduced by Rall (cf. chapter 2 of
this volume). Alternatively, it could obey a voltage-gated
differential equation.
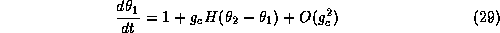
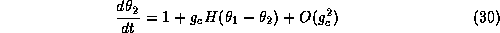
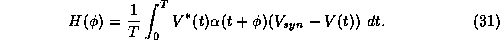
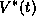 along with the synaptic
gating variable
along with the synaptic
gating variable 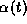 over one cycle for exactly the same
parameters as in
over one cycle for exactly the same
parameters as in 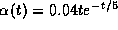 is an
``alpha'' function with a 5 msec time constant. Note the
similarity (except for scale) of the excitatory PRC and the
infinitesimal PRC,
is an
``alpha'' function with a 5 msec time constant. Note the
similarity (except for scale) of the excitatory PRC and the
infinitesimal PRC, 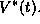 As with the PRC,
As with the PRC, 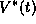 is mainly
positive showing that the predominant effect of depolarizing perturbations is
to advance the phase or equivalently speed up the oscillator.
In only a very small interval of time can the phase be delayed, and
this is a general property of membranes which become oscillatory through a
saddle-node bifurcation ([
is mainly
positive showing that the predominant effect of depolarizing perturbations is
to advance the phase or equivalently speed up the oscillator.
In only a very small interval of time can the phase be delayed, and
this is a general property of membranes which become oscillatory through a
saddle-node bifurcation ([
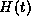 defined in equation (
defined in equation (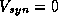 mV. We can
use this function along with equations (
mV. We can
use this function along with equations (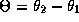 denote the phase difference between the two
oscillators. From equations (
denote the phase difference between the two
oscillators. From equations ( satisfies:
satisfies:
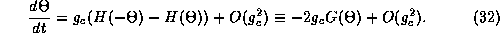
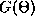 is just the odd part of the function H. Since the
coupling is weak, the higher order terms,
is just the odd part of the function H. Since the
coupling is weak, the higher order terms, 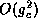 are ignored. Equation
are ignored. Equation
 does not change, that is, they are roots of
the function
does not change, that is, they are roots of
the function 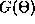 and they are stable fixed points if
and they are stable fixed points if
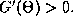 Since any odd periodic function has at least two
zeros,
Since any odd periodic function has at least two
zeros, 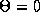 and
and 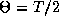 there will always exist
phase-locked states. However, these may not be stable, and there may
be others. Synchronous solutions (
there will always exist
phase-locked states. However, these may not be stable, and there may
be others. Synchronous solutions (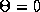 ) imply that both membranes fire
together. Anti-phase solutions (
) imply that both membranes fire
together. Anti-phase solutions (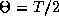 )
are exactly one half cycle apart.
Figure 14b shows the function
)
are exactly one half cycle apart.
Figure 14b shows the function 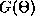 and from
this we see that there are 4 distinct fixed points: (i) the
synchronous
(precisely in-phase) solution, (ii) the anti-phase
solution, and (iii) a pair of phase-shifted solutions at
and from
this we see that there are 4 distinct fixed points: (i) the
synchronous
(precisely in-phase) solution, (ii) the anti-phase
solution, and (iii) a pair of phase-shifted solutions at
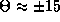 msec. Both the synchronous and anti-phase solutions
are unstable but the phase-shifted solution is stable. Thus, if two of
these oscillators are coupled with weak excitatory coupling and the
parameters chosen as above, they will phase-lock with a phase-shift of
about
msec. Both the synchronous and anti-phase solutions
are unstable but the phase-shifted solution is stable. Thus, if two of
these oscillators are coupled with weak excitatory coupling and the
parameters chosen as above, they will phase-lock with a phase-shift of
about 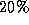 of the period.
Although the classical view is that mutual excitation leads to
perfect synchrony, computations with a variety of
neuronal models suggest that this is not generally the case.
of the period.
Although the classical view is that mutual excitation leads to
perfect synchrony, computations with a variety of
neuronal models suggest that this is not generally the case.