


Next: Oscillations emerging with
Up: Understanding Dynamics via
Previous: Understanding Dynamics via
Let's begin by considering the Morris-Lecar model in the case that there is a
unique rest state and a threshold-like behavior for action potential generation.
Figure 1A shows the V-responses to brief current pulses of different
amplitudes. The peak V is graded, but the variation occurs over a very narrow
range of stimuli; in this case, as in the standard HH model, the threshold
phenomenon is not discrete, but rather, steeply graded. In Figure 1B these same
responses are represented in the V-w plane. The solution path in the space of
dependent variables is called a trajectory, and direction of motion along a
trajectory is often indicated by an arrowhead. In Figure 1B, the flow is
generally counterclockwise. All the trajectories shown here ultimately lead to
the rest point: 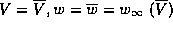 . One says that the rest state
is globally attracting. Each trajectory has a unique initial point, a
horizontal displacement from the rest point corresponding to instantaneous
depolarization by a brief current pulse. The trajectory of an action
potential shows the following features: an upstroke with rapid increase in V
(trajectory is moving rightward) and then the transient
plateau with a slower increase in
w corresponding to the opening of more
. One says that the rest state
is globally attracting. Each trajectory has a unique initial point, a
horizontal displacement from the rest point corresponding to instantaneous
depolarization by a brief current pulse. The trajectory of an action
potential shows the following features: an upstroke with rapid increase in V
(trajectory is moving rightward) and then the transient
plateau with a slower increase in
w corresponding to the opening of more 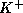 channels. When w is large
enough, the downstroke in V occurs - the trajectory moves leftward rapidly,
as V tends toward
channels. When w is large
enough, the downstroke in V occurs - the trajectory moves leftward rapidly,
as V tends toward 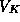 .
Finally, as w decreases (the potassium channels close)
the state point returns to rest with a slow recovery
from hyperpolarization.
.
Finally, as w decreases (the potassium channels close)
the state point returns to rest with a slow recovery
from hyperpolarization.
In the phase plane, the slope of a trajectory at a given point is 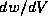 which
is just the ratio of
which
is just the ratio of 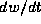 to
to 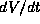 , and these quantities are evaluated
from the righthand sides of the differential equations
(4)-(5). (The program XPP has a command to
plot short vectors which indicate the flow pattern
generated by the equations. This allows a global view of the flow without
having to compute the trajectories. The program also computes
nullclines, defined next.) Thus a trajectory must
be vertical or horizontal where
, and these quantities are evaluated
from the righthand sides of the differential equations
(4)-(5). (The program XPP has a command to
plot short vectors which indicate the flow pattern
generated by the equations. This allows a global view of the flow without
having to compute the trajectories. The program also computes
nullclines, defined next.) Thus a trajectory must
be vertical or horizontal where 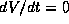 or
or 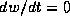 , respectively. These
conditions:
, respectively. These
conditions:
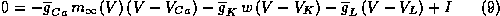
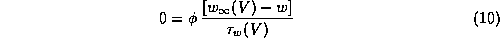
define curves, the V- and w-nullclines, which are shown dashed in
Figure 1B.
This provides a geometrical realization for where V and w can reach their
maximum and minimum values along a trajectory in the V-w plane; notice how the
trajectories cross the nullclines either vertically or horizontally in Figure
1B. The w-nullcline is simply the w-activation curve, 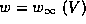 . The
V-nullcline, from equation (9), corresponds to V and w values at
which the instantaneous ionic current plus applied current is zero; below the
V-nullcline, V is increasing and above it, V is decreasing. The
cubic-like shape seen here reflects the N-shaped instantaneous I-V
relation,
. The
V-nullcline, from equation (9), corresponds to V and w values at
which the instantaneous ionic current plus applied current is zero; below the
V-nullcline, V is increasing and above it, V is decreasing. The
cubic-like shape seen here reflects the N-shaped instantaneous I-V
relation, 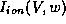 versus V with w fixed (equation (6)), which
is typical of excitable membrane models in which
the V-gated channels carrying inward current activate rapidly. From another
viewpoint, which is motivated by the slower time scale of w, suppose we fix
w, say, at a moderate value. Then the three points on the V-nullcline at
this w correspond to three pseudo-steady states; at the low-V state, small
outward and inward currents cancel while at the high-V state, both currents
are larger but are again in balance. These states are transiently visited
during the plateau phase and the return-to-rest phase of an action potential.
Notice how the trajectory is near the right and left branches of the
V-nullcline during these phases.
versus V with w fixed (equation (6)), which
is typical of excitable membrane models in which
the V-gated channels carrying inward current activate rapidly. From another
viewpoint, which is motivated by the slower time scale of w, suppose we fix
w, say, at a moderate value. Then the three points on the V-nullcline at
this w correspond to three pseudo-steady states; at the low-V state, small
outward and inward currents cancel while at the high-V state, both currents
are larger but are again in balance. These states are transiently visited
during the plateau phase and the return-to-rest phase of an action potential.
Notice how the trajectory is near the right and left branches of the
V-nullcline during these phases.
If 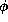 were smaller still, then the phase plane trajectories (except when
near
the V-nullcline) would be nearly horizontal (since
were smaller still, then the phase plane trajectories (except when
near
the V-nullcline) would be nearly horizontal (since 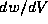 would be small).
In this case, the action potential trajectory during the plateau and recovery
phases would essentially cling to, and move slowly along, either the right or
left branch of the V-nullcline. The downstroke would occur at the knee of the
V-nullcline. The time course would be more like that of a cardiac action
potential. Also, in the case of smaller
would be small).
In this case, the action potential trajectory during the plateau and recovery
phases would essentially cling to, and move slowly along, either the right or
left branch of the V-nullcline. The downstroke would occur at the knee of the
V-nullcline. The time course would be more like that of a cardiac action
potential. Also, in the case of smaller 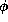 , the threshold phenomenon would
be extremely steep; the middle branch of the V-nullcline would act as an
approximate separatrix between sub- and super-threshold initial conditions. In
contrast, for larger
, the threshold phenomenon would
be extremely steep; the middle branch of the V-nullcline would act as an
approximate separatrix between sub- and super-threshold initial conditions. In
contrast, for larger 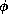 , the response amplitude is more graded.
This theoretical conclusion led to an experimental
demonstration
for squid axon [3] that, at higher temperatures, the action
potential
does not behave in an ``all-or-none'' manner.
, the response amplitude is more graded.
This theoretical conclusion led to an experimental
demonstration
for squid axon [3] that, at higher temperatures, the action
potential
does not behave in an ``all-or-none'' manner.
We remark that phase plane methodology applies to systems which are autonomous,
i.e. in which there is no explicit time dependence in the equations. This
means that the nullclines and flow field do not change with time. This could
not be done if, for example, I were periodic in t; the treatment
of periodic
stimuli will be covered later. However, the phase plane method
extends to cases
where a step change in a parameter occurs.
At the time a parameter's value jumps, the nullclines would change
instantaneously, but not the present location of V and w.
FitzHugh [11] uses this trick to interpret anodal break
excitation and
Somers and Kopell [33] have used this to analyze the behavior of coupled
Morris-Lecar oscillators when 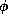 is very small.
is very small.


Next: Oscillations emerging with
Up: Understanding Dynamics via
Previous: Understanding Dynamics via
Bard Ermentrout
Mon Jul 29 17:47:46 EDT 1996
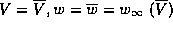 . One says that the rest state
is globally attracting. Each trajectory has a unique initial point, a
horizontal displacement from the rest point corresponding to instantaneous
depolarization by a brief current pulse. The trajectory of an action
potential shows the following features: an upstroke with rapid increase in V
(trajectory is moving rightward) and then the transient
plateau with a slower increase in
w corresponding to the opening of more
. One says that the rest state
is globally attracting. Each trajectory has a unique initial point, a
horizontal displacement from the rest point corresponding to instantaneous
depolarization by a brief current pulse. The trajectory of an action
potential shows the following features: an upstroke with rapid increase in V
(trajectory is moving rightward) and then the transient
plateau with a slower increase in
w corresponding to the opening of more 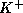 channels. When w is large
enough, the downstroke in V occurs - the trajectory moves leftward rapidly,
as V tends toward
channels. When w is large
enough, the downstroke in V occurs - the trajectory moves leftward rapidly,
as V tends toward 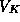 .
Finally, as w decreases (the potassium channels close)
the state point returns to rest with a slow recovery
from hyperpolarization.
.
Finally, as w decreases (the potassium channels close)
the state point returns to rest with a slow recovery
from hyperpolarization.
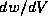 which
is just the ratio of
which
is just the ratio of 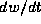 to
to 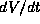 , and these quantities are evaluated
from the righthand sides of the differential equations
(
, and these quantities are evaluated
from the righthand sides of the differential equations
(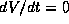 or
or 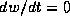 , respectively. These
conditions:
, respectively. These
conditions:
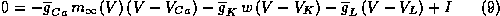
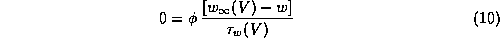
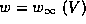 . The
V-nullcline, from equation (
. The
V-nullcline, from equation (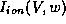 versus V with w fixed (equation (
versus V with w fixed (equation (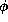 were smaller still, then the phase plane trajectories (except when
near
the V-nullcline) would be nearly horizontal (since
were smaller still, then the phase plane trajectories (except when
near
the V-nullcline) would be nearly horizontal (since 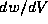 would be small).
In this case, the action potential trajectory during the plateau and recovery
phases would essentially cling to, and move slowly along, either the right or
left branch of the V-nullcline. The downstroke would occur at the knee of the
V-nullcline. The time course would be more like that of a cardiac action
potential. Also, in the case of smaller
would be small).
In this case, the action potential trajectory during the plateau and recovery
phases would essentially cling to, and move slowly along, either the right or
left branch of the V-nullcline. The downstroke would occur at the knee of the
V-nullcline. The time course would be more like that of a cardiac action
potential. Also, in the case of smaller 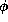 , the threshold phenomenon would
be extremely steep; the middle branch of the V-nullcline would act as an
approximate separatrix between sub- and super-threshold initial conditions. In
contrast, for larger
, the threshold phenomenon would
be extremely steep; the middle branch of the V-nullcline would act as an
approximate separatrix between sub- and super-threshold initial conditions. In
contrast, for larger 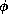 , the response amplitude is more graded.
This theoretical conclusion led to an experimental
demonstration
for squid axon [
, the response amplitude is more graded.
This theoretical conclusion led to an experimental
demonstration
for squid axon [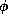 is very small.
is very small.