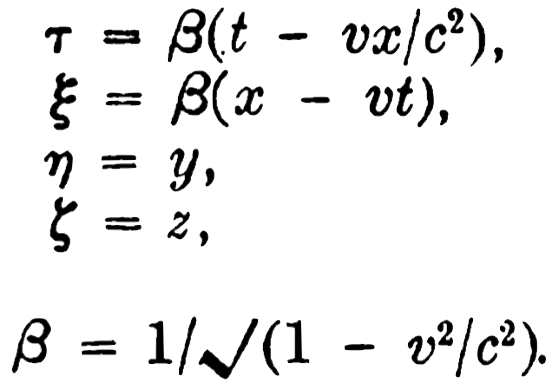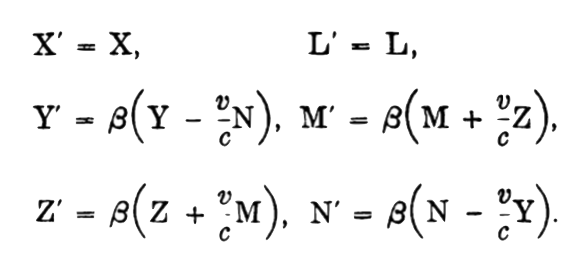HPS 1632 Einstein for Almost Everyone
Fall term 2019Back to course document list.
Reading Assignments
Nuggets: A nugget is some item in the reading that strikes you as noteworthy. It might be a clever remark; or an unexpectedly clever insight; or just something that piqued your interest.
1. Special Relativity, Part 1.
Read the introduction and I. Kinematical Part (Sections 1 to 4) of A. Einstein, "On the Electrodynamics of Moving Bodies" In Principle of Relativity
What is Einstein's statement of the principle of relativity?
What is Einstein's statement of the light postulate?
What are the main results of each section?
For submission:
A nugget
What is the problem outlined in Section 1 about comparing the timing of events at a point A in space with those of a point B in space?
The most important result of Part I is the Lorentz transformation,
derived in Section 3:
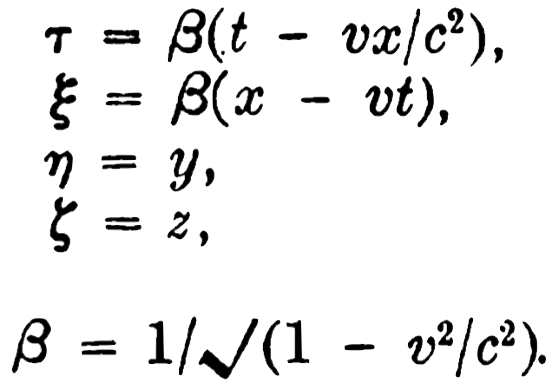
What is represented by the variables t, x, y, z, τ, ξ, η ζ ?
1. Special Relativity, Part 2.
Read: "Chasing the Light: Einstein's Most Famous Thought Experiment," Thought Experiments in Philosophy, Science and the Arts, eds., James Robert Brown, Mélanie Frappier and Letitia Meynell, New York: Routledge, 2013. pp. 123-140.
For submission:
A nugget
In a 19th century ether theory of light, how would a light beam appear if you chase after it at the speed of light?
A field quantity φ in a plane wave propagating in the x direction has
a time dependency
φ(x, t) = f(x - ct)
for some function f, where c is the speed of light and x and t are the
usual coordinates. The classical "Galilean coordinate transformation is
x' = x-vt, t'=t, y'=y, z'=z,
where the coordinates have their usual meanings and primes denote those
attached to a frame of reference moving at v in the +x direction with
respect to the unprimed frame of reference.
Transform the expression for φ to demonstrate your answer.
(For simplicity, assume φ is a scalar so that φ'=φ.)
1. Special Relativity, Part 3.
Read Section 6 "Transformation of the Maxwell-Hertz Equations for Empty Free Space..." in II. Electrodynamic Part of A. Einstein, "On the Electrodynamics of Moving Bodies" In Principle of Relativity.
What are the main results of the section?
What is the point made concerning the "old manner of expression" and "new
manner of expression" a the end of Section 6? (Hint: is there a connection
to the magnet and conductor thought experiment of the introduction?)
For submission:
A nugget
In Einstein's stationary frame of reference "K", the electric field has
components (X, Y, Z) and the magnetic field has components (L, M, N). In
Einstein's inertially moving frame of reference "k," they have
components (X', Y', Z') and (L', M', N') respectively. The Lorentz
transformation equations that relate them are:
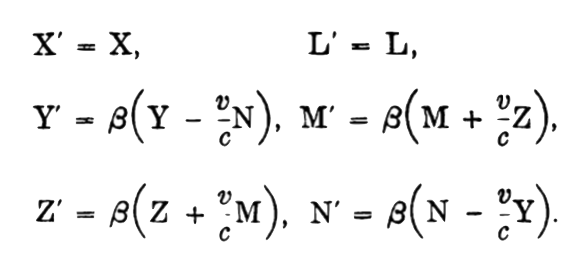
How do these equation "mix up" electric and magnetic fields? e.g. start with a magnetic field but no electric field in k. That is, X'=Y'=Z'=0, but L', M' and N' need not be zero. What happens when we describe this situation from the "stationary" frame K?
1. Special Relativity, Part 4.
What are the main results of the sections?
What are Doppler's Principle and the effect of [stellar] aberration? Look them up, if you need to!
How does Einstein arrive at the conclusion in Section 10 that "Velocities greater than that of light have--as in our previous results--no possibility of existence."
For submission:
A nugget
We define force in Newtonian physics as "F=ma": force = mass x acceleration, where a = acceleration = d2/dt2 x. Sometimes we use a different formulation "F = d/dt (mv)": force = rate of chance of momentum mv = m(dx/dt). In Newtonian physics, the two definitions are equivalent.
(a) Show this equivalence
This equivalence fails in relativity theory since mass m(v) changes with speed v.
(b) Show that the two formulae for force now give different results.
Hint: apply the product rule of
differentiation to F = d/dt(mv) and find an extra term.
(c) Which formula is used by Einstein in his analysis?
Bonus optional hard question: Why does Einstein restrict the analysis to slowly accelerated electrons? (He does not explain why in the text.)
1. Special Relativity, Part 5
Einstein read philosophers and used their ideas to help him in his physics. To see one important example, read "How Hume and Mach Helped Einstein Find Special Relativity." (You have already seen the content of Section 2, so you can just skim over it.)
For submission
A nugget
The doctrine of operationism says that the meaning of a concept just is the operations used to measure it. For example to say someone has an IQ of 120 just means that they score 120 on an IQ test and nothing more. This doctrine was described in detail after Einstein's work on relativity by Percy Bridgman. Einstein's work was an important motivation for him. (For more, if you want it, see 4. Operationism (P. W. Bridgman).)
Read the (short!) Chapter 8 of Einstein's popular text on relativity. How in it does Einstein give an analysis that would be inspiring to operationists?
1. Special Relativity, Part 6.
A. Einstein, "Does the Inertia of a Body Depend Upon its Energy-Content"
(1905) in Principle of Relativity.
and
Section 1 "A Special Case" in A. Einstein, "The
Principle of Conservation of Motion of the Center of Gravity and the
Inertia of Energy," (1906) Doc. 35 in Einstein Papers, Vol
2.
What precisely is demonstrated in each paper?
For submission
A nugget
The speed of light "c" does not appear in Einstein's 1906 paper. What symbol does he use for the speed of light?
Describe one difference between the 1905 and 1906 derivations.
2. Minkowski Spacetime
Read Spacetime,
Spacetime and
the Relativity of Simultaneity
and (optionally) Spacetime,
Tachyons, Twins and Clocks
Then take a look at the notes (Notes on metrical spaces, Notes on Minkowski spacetime) and see if you can match up the equations in the notes with qualitative discussion above.
Can you recover these results:
From the Euclidean line element, show that the locus of points
equidistant from the origin in a circle.
From the Minkowski line element, show that the locus of points
equi-interval from the origin is a hyperbola.
For submission
A nugget
Two inertial observers A and B are in relative motion. Draw two spacetime diagrams that show their worldlines and their associated hypersurfaces of simultaneity in
(a) a Minkowski spacetime
(b) a Newtonian spacetime
Neatness matters in diagrams. Take trouble to draw figures that are tidy and convey their content clearly. I will deduct points for hasty or messy diagrams.
3. General Relativity, Part 1.
Read General Relativity.
Then take a look at the notes (Notes on tidal acceleration, Notes on general relativity) and see if you can match up the equations in the notes with the qualitative discussion above.
For submission
A nugget
A homogeneous gravitational field has a potential φ=gx. It accelerates free bodies in the -x direction.Neatness matters in proofs. Take the trouble and explain clearly each step. I will deduct points for hasty or messy work.
3. General Relativity, Part 2.
Read
Then take a look at the notes ( Notes on general relativity) and see if you can match up the equations in the notes with the qualitative discussion above.
For submission
A nugget
If we ignore the geometric curvature of the spatial sections, the line
element of spacetime in the vicinity of the sun is roughly approximated
by
ds2 = - (c2 + 2φ)dt2 + dx2 +
dy2 + dz2
where the potential φ becomes more negative the closer the we get to the
sun, whose center is at x=y=z=0.
From this line element compute the coordinate velocities of
light dx/dt, dy/dt and dz/dt and show that they are equal.
(How? To find dx/dt, set ds = 0 and also dy=dz=0. Then solve for dx divided by dt.)
Optional bonus harder question: If the speed of light is same
in all directions near the sun, how it is possible that starlight is
deflected by the sun?
Hint: How does light get refracted in media of varying optical density,
such as when mirages form?
Optional bonus even harder question: why are dx/dt, etc. only coordinate velocities? How do they differ from "real" velocities?
Neatness matters...
3. General Relativity, Part 3.
Read Einstein's Pathway to General Relativity, Einstein, "Foundation of the General Theory of Relativity," 1916, Part A
Notice how the steps of the history of Einstein's discovery as recounted in "...Pathway..." reappear as the logical foundation of the theory in Einstein's 1916 paper.
For submission
A nugget
On p.117 of "Foundation ...," Einstein concludes that "We therefore reach this result:--In the general of relativity, space and time cannot be defined in such a way that differences of the spatial co-ordinates can be directly measured by the unit measuring-rod, or differences in the time co-ordinate by a standard clock."Neatness matters...