::: center home >> being here >> last donut? >> cosmic confusions |
Cosmic Confusions
The Oxford conference assembled both cosmologists and philosophers, motivated by the idea that philosophers of science might well be useful to cosmologists. That idea is laudable in the abstract, but quite intimidating in practice. In a mere 40 minutes, I had to convince the assembled multitude of cosmic luminaries that our philosophical cleverness is actually useful to them. I opened my talk with the quip that the word philosopher means lover of wisdom. "But that doesn't mean we have any." It got a little laugh. The cosmologist Sean Carroll, one of our Annual Lecture Series speakers from a past year, was "live blogging" the event for Discover magazine. Throughout, we watched him tapping on his keyboard, wondering just how our last ill-considered remark might be reported. Alas, the talk did not go well. I had worked hard to compress my material down to 40 minutes and thought I might just get through it in that time, barely. Then, as I stood at the podium preparing for my "wisdom" quip, the session chair informed me brightly: "So it's 30 minutes and 10 for questions." My stomach dropped. There was no time to argue or time left to decide what to cut. So off I went, successfully blasting through a much longer talk in 30 minutes. I suspected my pace had produced buffer overflows across the hall. I knew it had, when, in an open discussion session, one of the string theorists asked memorably why I wanted to undo the Enlightenment.
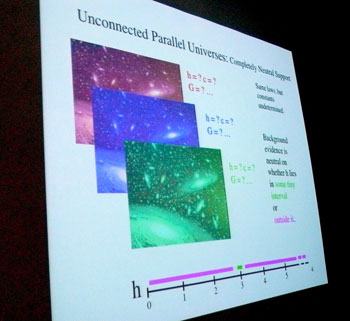
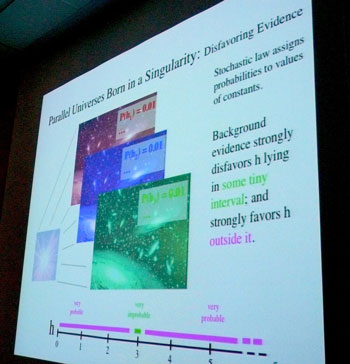
To get a sense of how this works, here's the introductory example I used. Imagine that your multiverse theory posits that there there are many parallel universes, completely unconnected from ours. They all have the same fundamental laws, but we have no idea of the numerical values of the constants h, c, G, ... in each of them. Then we have the same, neutral support for a value of h between 0 and 1 and between 1 and infinity. That last claim may seem odd to you. Should we have the same support for a finite interval of values as for an infinite interval? The oddness goes away if you imagine inductive support for values of the inverse of h, that is 1/h. That h lies in the finite interval from 0 and 1 corresponds to an infinite range of values of 1/h; and the infinite range of 1 to infinity for h corresponds to a finite range of values for 1/h, that is, 0 to 1. That was the case of neutral support. Now take a different case. Imagine that a new theory tells us that these universes are born from a singularity and that the law governing their emergence assigns probabilities to the different values of the fundamental constants. (This is not standard cosmology. It is just an imagined theory not so remote from what real multiverse theorists do entertain.) In this case, we might reasonably expect a fairly widely spread probability distribution on h. Then the probability of h in the interval from 0 to 1 will be small; and its probability in the range 1 to infinity very high. The small probability for the interval 0 to 1 shows that our background strongly disfavors the interval. The danger is that the two cases of neutral and disfavoring support are conflated. If you invariably think of inductive support probabilistically, it can be hard even to see that the two cases are different. Then, when you confuse the second for the first, you introduce spurious results that are purely artifacts of the poor choice of an inductive logic. Let's look at an inductive fallacy that arises from the conflation. We might try to represent neutral evidential support by saying that the probability is very small--say 0.01--of finding h in 0 to 1, or h in 1 to 2, or h in 2 to 3, and so on. Now start combining these outcomes, each of low probability 0.01. As we "or" more together to form greater intervals, we add their probabilities. Eventually we end up assigning a very high probability 0.99 for h in the interval 0 to 99. So we would now say a value in that range is strongly supported. That's the fallacy. If you genuinely have a case of neutral support, you have no more support for h lying in 0 to 1 than in 0 to 99. You just have no evidence pointing any which way. Would anyone really commit this last inductive fallacy? It turns out that there are many cases of it in the literature. Van Inwagen, for example, asks the metaphysician's favorite question, why is there anything at all. He notes that there is one way for nothing to be; but there are infinitely many ways different beings can come about. Our background assumptions are so bare that they bear neutrally on each of these ways. However, if we now rather thoughtlessly distribute probabilities over all these cases somewhat uniformly, we conclude that all the probability mass goes to the cases of being and the case of nothing is "as improbable as anything can be." That is a quote. Ouch! Adolf Gruenbaum has widely and effectively decried the confusions surrounding what he calls the "primordial existence question." He was sitting in the frontmost chair and I announced that I was presenting this example in his honor. There was still a lot more to say. There are more examples of this inductive fallacy; and a lot of complaints about the "doomsay argument," which commits a similar fallacy; and more. If you want to hear about it, see my "Cosmic Confusions: Not Supporting versus Supporting Not-" on my website. The talk was now over. The room was very full. I found out later from Dennis and Carol that all the coffee was gone, all the donuts were eaten and there was just a half of a toasted bagel left lying over the toaster. It was a clean sweep on the donut-bagel scale. The audience had seemed receptive, but how would they react? The first to come up to me in the break was one of our more senior graduate students. I knew he had drunk deep and satisfying draughts of Bayesianism. He had to rush out to teach, but wanted me to know that he disagreed and that I just didn't understand modern Bayesianism. As he started to sketch the fatal omission he'd found, my heart sank in despair. It was a simple misreading of what I'd said. It metamorphised my objections into one that Bayesians could answer. I'd heard it before. Was it possible that I'd expressed myself so poorly? How better could I express myself so Bayesians can actually hear what I say and not some garbled version of what they'd like me to say?
As the room was clearing, I really only had one thought. Had I repeated the debacle of Oxford? Had I spoken too fast? I asked several of our Fellows. They each gave the same answer: no, not at all. But they each answered the same way, with a slight pause first, in which I was sure they were deciding not to say that it was pretty quick but they could keep up. However they did tell me that it was quite convincing and also quite enjoyable. I'm not sure which was more gratifying. John D. Norton |