How to Teach Science in an HPS Class

For my session of the teaching practicum, I will address the question of how one goes about teaching the content of a science in the context of an HPS class. I will describe a technique that has proven useful for the sorts of classes I teach. It may not be applicable in all types of classes. However it has the virtue of being clearly describable and quite portable.

The default way of teaching a science is to relate to the students a body of fact. Know this, and this, and this, and so on. The better way is to give the students a sense that the many facts of the science are connected together into a logical structure. That means that they you know one part of it, they can navigate to other parts of the structure or even build new parts.

The idea is to provide the students with a simple but versatile tool that lets them navigate through the structure for themselves. The emphasis is on choosing the most versatile tool you can find. Then they have one trick that it has multiple uses.

Here are several examples:

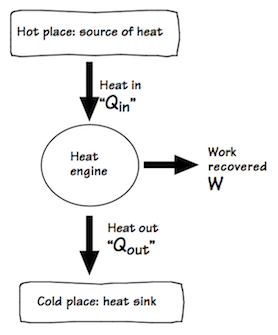
1. A graphical method for inferring results in the thermodynamics of heat engines.

Quite powerful and general results can be recovered merely by fitting together figures like the one above, jigsaw puzzle style. The example is drawn from Ch.6-8 of my text How Science Works, which is used in HPS 0621 Problem Solving.

2. A simple formula for computing of the standard deviation of the outcome of Bernoulli/binomial trials.

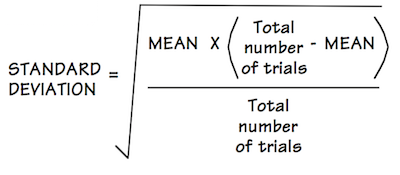
This one formula can be applied to many different problems in statistical analysis to decide whether some effect is significant or merely a random fluctuation. The example is drawn from Ch.10-12 of my text How Science Works, which is used in HPS 0621 Problem Solving.

3. The relativity of simultaneity.

Special relativity seems paradoxical on first contact. Two observers in relative motion each judge the others' clock to be slowed down. How can both judge this? The key to seeing past the problem is to recognize the relativity of simultaneity. Until this notion is understood, nothing really makes sense in relativity theory. Once it is understood, almost all puzzles dissolve.

See Einstein for Everyone. Look at the chapters: "Special Relativity: Relativity of Simultaneity" and "Is Special Relativity Paradoxical?"

4. Spacetime diagrams.

Grasping the relativity of simultaneity is itself arduous, until one learns how to represent it in a spacetime diagram These diagrams are in turn a powerful technique for understanding the logical structure of special relativity.

See Einstein for Everyone. Look at the chapters: "Spacetime and the Relativity of Simultaneity" and "Spacetime, Tachyons, Twins and Clocks."

5. Geodesic deviation.

General relativity is, reputedly, a very difficult theory to learn. Part of the problem is that its basic ideas are commonly presented poorly to non-technical audiences. After much experiment and a few spectacular failures, I found an effective way to develop real comprehension of the key ideas. It uses a single, versatile tool: the notion of geodesic deviation.

See Einstein for Everyone. Look at the chapter: "General Relativity."

6. Conformal diagrams.

Black holes are pathological structures in spacetime with fascinating global structures. They open doorways to other universes. Grasping the spacetime geometry of such structures is quite difficult. That is, it is so until one learns a simple diagrammatic technique, conformal diagrams.

See Einstein for Everyone. Look at the chapter: "A Better Picture of Black Holes."

Your Assignment

Before the practicum meeting, identify some piece of science that you might like to teach in an HPS class. Consider how you might teach it. You may find the above technique useful. Or it may not be useful. Be prepared to describe your ideas briefly to the practicum.

To help you get started, think about:

1. What it is that the students already know.

2. What is the minimum you need to add to that so that they are informed of the science in a way that is useful to your further HPS teaching goals.